Дан треугольник, в котором известен полупериметр p и сторона a.
Найти: длину касательной AN = x.
Ответы
Ответ дал:
2
Ответ:
в додатку (п'яте фото)
Объяснение:
1. Проведем биссектрисы и получим центр вписанной окружности O.
2. Из точки O опустим перпендикуляры на стороны и получим точки касания:
ON⊥AB,
OL⊥AC,
OK⊥BC.
ð N, K, L – точки касания.
3. Отметим равные касательные x, y, z.
4. Напишем связь между сторонами треугольника и касательными.
Сложим 3 соотношения:
Для прямоугольного треугольника аналогично выводится формула для радиуса вписанной окружности (в который превращается один из отрезков касательных):
первые фото выходят соотношения....
и последняя - ответ
Приложения:
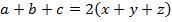
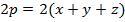
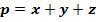
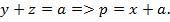
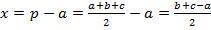
Аноним:
https://prnt.sc/8A3cjrmV0N0N
это ссылка на рисунок к задаче. Знания больше 5 фоток не грузят.
просто перейди по ссылке, откроется фото к задаче
Большое спасибо:)
Похожие вопросы
1 год назад
1 год назад
2 года назад
2 года назад