ПОСЛЕДНИЕ 100 БАЛЛОВ!

1. В рівнобічній трапеції з гострим кутом 60˚ бісектриса цього кута ділить меньшу основу, рівну 16 см, навпіл. Знайдіть середню лінію трапеції.
8класс поясніте на 8 класс а не на студента
последніе 100 баллов

detkikz6: что нужно а как вам не стыдно а??????

Аноним: что мне нестыдно лох

Аноним: и не указывай мне

Ответы

Ответ дал: natalyabryukhova

Ответ:

Средняя линия трапеции равна 20 см(

Объяснение:

1. В равнобедренной трапеции с острым углом 60 биссектриса этого угла делит меньшее основание, равное 16 см, пополам. Найдите среднюю линию трапеции.

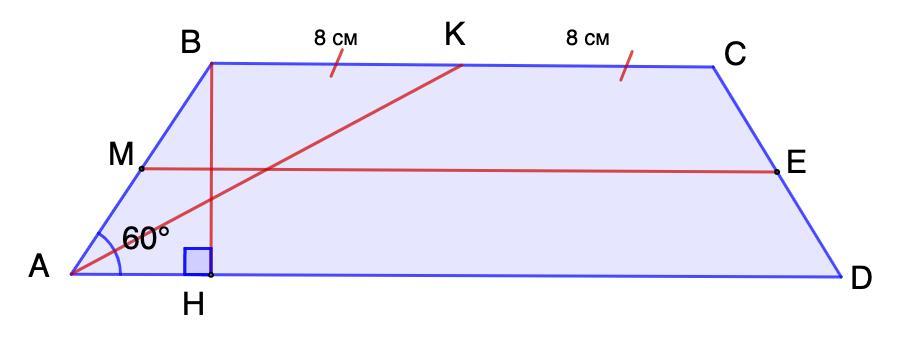
Дано: ABCD - равнобедренная трапеция;

∠А = 60°;

ВС = 16 см;

ВК = КС;

АК - биссектриса.

Найти: Среднюю линию трапеции МЕ.

Решение:

Проведем ВН - высота.

ВК = КС = 16 : 2 = 8 (см)

1. Рассмотрим ΔАВК.

∠ВАК = ∠КАD = ∠А : 2 = 30° (АК - биссектриса)

∠АКВ = ∠КАD (накрест лежащие при ВС || AD и секущей АК)

⇒ ∠ВАК = ∠АКВ

Если в треугольнике два угла равны, то треугольник равнобедренный.

⇒ ВК = АВ = 8 см

2. Рассмотрим ΔАВН - прямоугольный.

Сумма острых углов прямоугольного треугольника равна 90°.

⇒ ∠АВН = 90° - 60° = 30°

Катет, лежащий против угла в 30°, равен половине гипотенузы.

⇒ АН = АВ : 2 = 4 см.

3. Воспользуемся свойством равнобедренной трапеции.

Высота, опущенная из вершины тупого угла равнобедренной трапеции на большее основание, делит его на части, меньшая из которых равна полуразности оснований.

$\displaystyle AH=\frac{AD-BC}{2}\\ \\4=\frac{AD-16}{2}\\ \\AD-16=8\\\\AD=24$