Предмет: Алгебра
Автор: sdhjfsdhjfsdhjfhj
Вопрос задан 1 год назад

< >

ОТДАЮ ВСЕ БАЛЛЫ! СДЕЛАЮ ЛУЧШИМ ОТВЕТОМ!
Найдите первообразную функций:

Приложения:

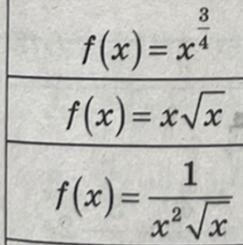
MizoriesKun: Это же табличные значения

sdhjfsdhjfsdhjfhj: Я в алгебре не разбираюсь, помогите пожалуйста :(

sdhjfsdhjfsdhjfhj: какие это значения? F(x) =

Ответы

Ответ дал: MizoriesKun

1

Смотри................

Приложения:

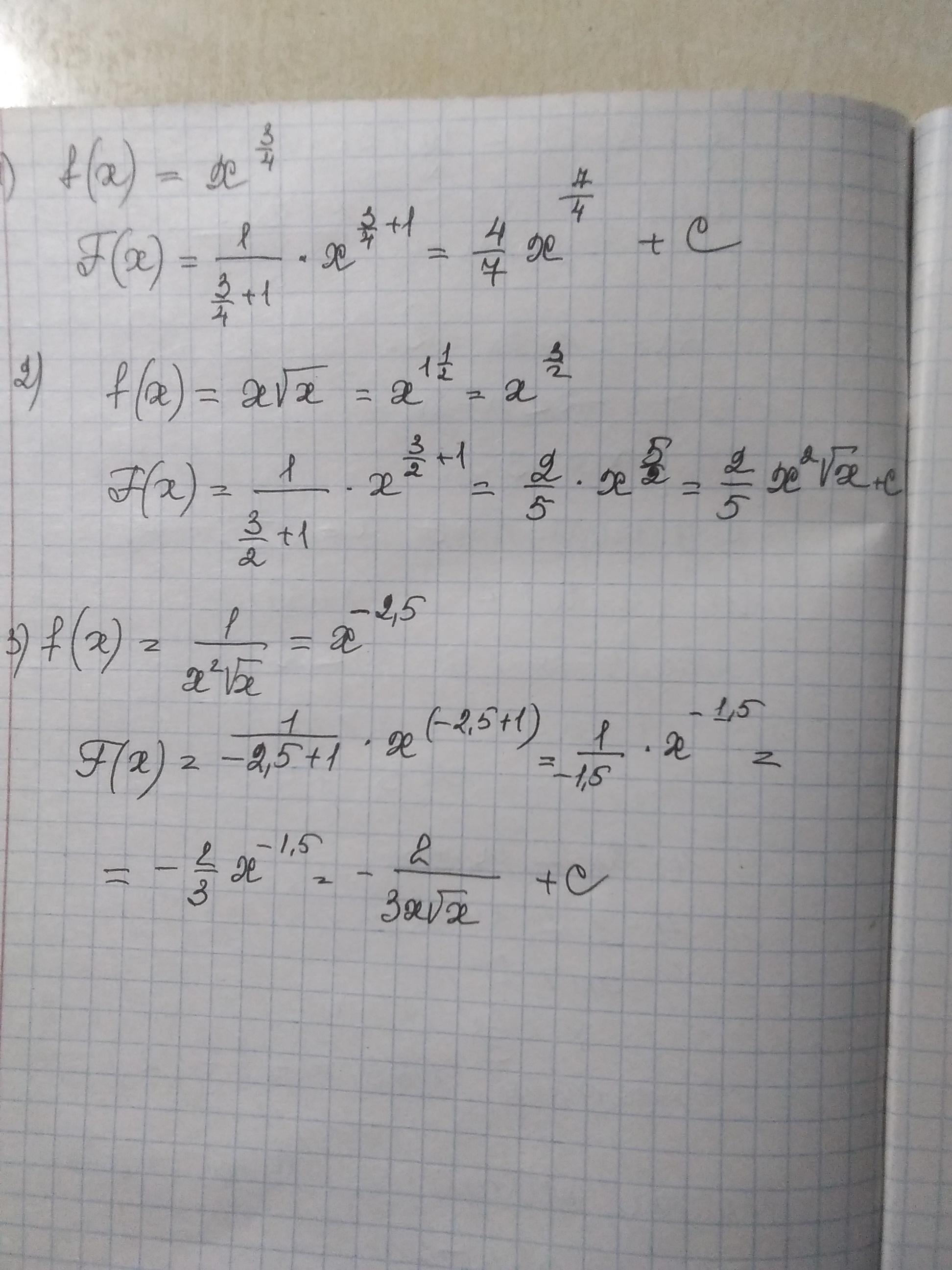
Ответ дал: Universalka

1

$\displaystyle\bf\\1)\\\\f(x)=x^{\frac{3}{4} } \\\\F(x)=\frac{4}{7} x^{\frac{7}{4} } +C\\\\\\F(x)=\frac{4}{7} \sqrt[4]{x^{7} } +C\\\\\\\boxed{F(x)=\frac{4}{7} x\sqrt[4]{x^{3} } +C}\\\\\\2)\\\\f(x)=x\sqrt{x} =x\cdot x^{\frac{1}{2} } =x^{\frac{3}{2} } \\\\\\F(x)=\frac{2}{5} x^{\frac{5}{2} } +C\\\\\\F(x)=\frac{2}{5} \sqrt{x^{5} } +C\\\\\\\boxed{F(x)=\frac{2}{5} x^{2} \sqrt{x} +C}\\\\3)$

$\displaystyle\bf\\f(x)=\frac{1}{x^{2} \sqrt{x} } =\frac{1}{x^{2} \cdot x^{\frac{1}{2} } }=\frac{1}{x^{\frac{5}{2} } } =x^{-\frac{5}{2} } \\\\\\F(x)=-\frac{2}{3} x^{-\frac{3}{2} } +C\\\\\\F(x)=-\frac{2}{3} \cdot \frac{1}{x^{\frac{3}{2} } } +C\\\\\\\boxed{F(x)=-\frac{2}{3x\sqrt{x} } +C}$

Похожие вопросы

Русский язык

1 год назад

3. Распредели и запиши имена сущ. в тетрадь по группам: 1) название качеств человека; 2) название состояний человека; 3) название промежутков времени; 4) название действий. Каникулы, смелость,

Математика

1 год назад

У двоцифровому числi кiлькiсть десятків на 2 менша від кiлькостi одиниць. Якщо цифри числа переставити, то отримане число буде в 1, 3/4 раза більшим за дане. Знайдіть дане двоцифрове число.

Английский язык

1 год назад

пиши что хочешь сщпсщпсщпс

Алгебра

1 год назад

Використовуючи графік функції на малюнку, заповніть таблицю: надо ещё нарисовать

Литература

2 года назад

Почему Самсон Вырин не порадуется за дочь, которая приобрела более высокое материальное положение? быстрей пожалуйста

Физкультура и спорт

2 года назад

Каким образом атакующий игрок может избежать блокировки защитников? Верных ответов: 3 применять обманные движения выполнять бросок в падении выполнять свободный бросок выполнять бросок в прыжке

Математика

8 лет назад

Найдите два составных числа игрик(у), которое удовлетворяют неравенству 71< у <79 Как решать? Не понимаю

Физика

8 лет назад

Движение материальной точки описывается уравнением x=5-2t+4t2. Приняв её массу равной 1,5кг, найдите импульс через 3с после начала движения.