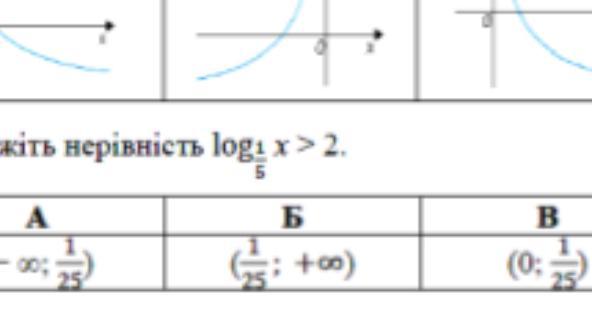• Предмет: Алгебра
  • Автор: karinkamandari28288
  • Вопрос задан 1 год назад
< >

Розв‘яжіть нерівність log1/5x>2
Срочно!!

Приложения:

Ответы

Ответ дал: flybirdster
1

Ответ: B

          (0;\displaystyle\frac{1}{25} )

Объяснение:

Запишем неравенство:

log_{\frac{1}{5} } x &gt; 2

Правую часть неравенства приводим к логарифму. Для этого воспользуемся формулой b=log_{a} a^{b}:

log_{\frac{1}{5} } x &gt; log_{\frac{1}{5} } (\displaystyle\frac{1}{5} )^{2}

Теперь логарифмы в обеих частях одинаковы, поэтому их можно пренебречь. Но так как основание меньше 1, то знак поменяет направление:

x &lt; (\displaystyle\frac{1}{5} )^2

x &lt; \displaystyle\frac{1^2}{5^2}

x &lt; \displaystyle\frac{1}{25}

Чтобы выражение log_{\frac{1}{5} }x имело смысл х должен быть больше нуля:

x &gt; 0

Пересечение x &lt; \displaystyle\frac{1}{25} и x &gt; 0 дает (0; 1/25).

Поэтому решением неравенства будет вариант В:

(0;\displaystyle\frac{1}{25} )

Похожие вопросы
Литература
1 год назад
Просвітництво як філософсько - ідеологічна течія та місце Й.В.Гете у ньому.
Українська література
1 год назад
11. Визначте художньо-виражальні засоби в наведеному фрагменті твору. Поясніть їхню роль. «Без милого долi нема. // Стане свiт тюрмою, // Без милого щастя нема. // Нема і спокою.​
Українська мова
1 год назад
Провідміняй дату свого народження, записавши її словосполученням числівника з іменником. 15 липня
История
1 год назад
Порівняйте вигляд давніх і сучасних будинків plisssssssss
Английский язык
2 года назад
решите пожалуйста даю 40 баллов​
Українська мова
2 года назад
12 речень з прямою мовою з художньої літератури
Геометрия
8 лет назад
Найдите сторону треугольника лежащую против угла в 135 градусов,если две другие стороны равны по 3 см
Геометрия
8 лет назад
Укажите номер рисунка,на котором изображена средняя линия треугольника