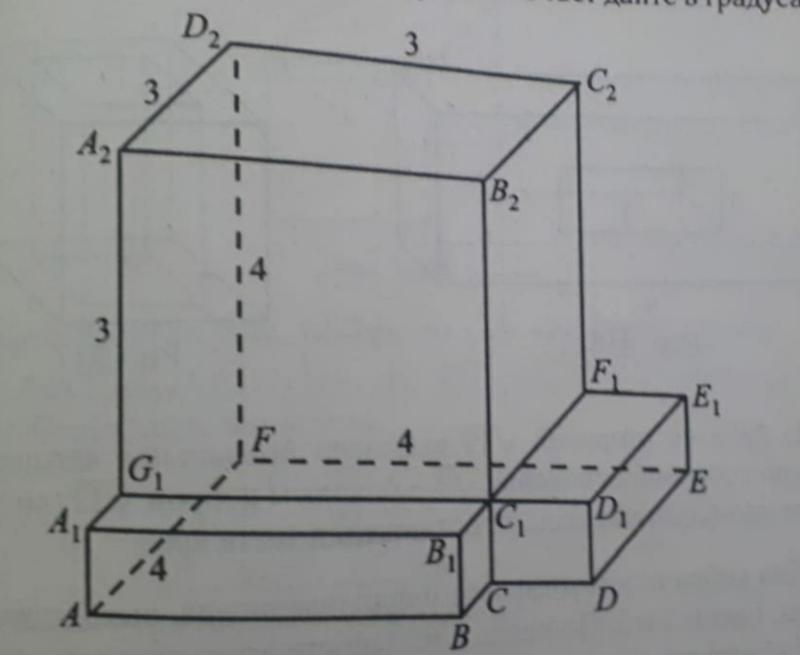
Найдите угол AED₂ многогранника, изображённого на рисунке. Все двугранные углы многогранника прямые. Ответ дайте в градусах. НАПИСАТЬ ПОДРОБНОЕ РЕШЕНИЕ.

Ответ:

∠AED2=60°

Объяснение:

∆D2FE- прямоугольный треугольник.

По теореме Пифагора:

D2E=√(D2F²+FE²)=√(4²+4²)=4√2

∆D2FA- прямоугольный треугольник.

По теореме Пифагора:

D2A=√(D2F²+FA²)=√(4²+4²)=4√2

∆AFE- прямоугольный треугольник

По теореме Пифагора:

АЕ=√(АF²+FE²)=√(4²+4²)=4√2

∆D2AE- равносторонний треугольник, все стороны равны 4√2.

В равностороннем треугольнике все углы по 60°

∠АЕD2=60°