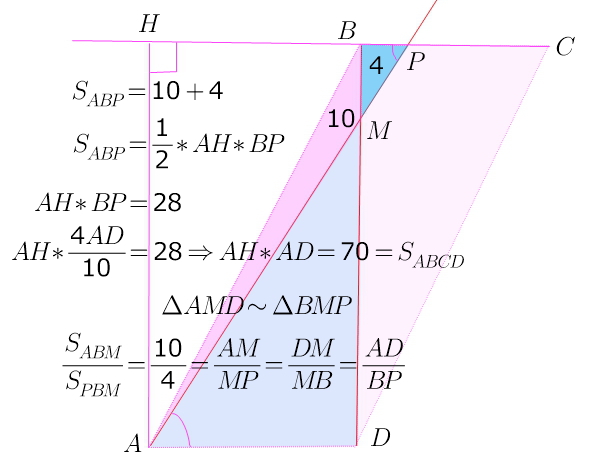
Из вершины параллелограмма АВСD проведен луч, который пересекает сторону ВС в точке Р, а диагональ ВD в точке М. Площадь треугольника АВМ равна 10, а площадь треугольника ВМР равна 4. Найдите площадь параллелограмма.

площадь параллелограмма=произведению
стороны на высоту, проведенную к этой стороне: AH*AD = AH*BC
площади данных треугольников относятся как основания АМ:МР,
т.к. эти треугольники имеют равные высоты)))
если рассмотреть треугольники, содержащие АМ и МР, то
окажется, что они подобны с коэффициентом k = 10/4
т.е. ВР = 0.4*BC
площадь параллелограмма = 70