Предмет: Геометрия
Автор: Morook
Вопрос задан 1 год назад

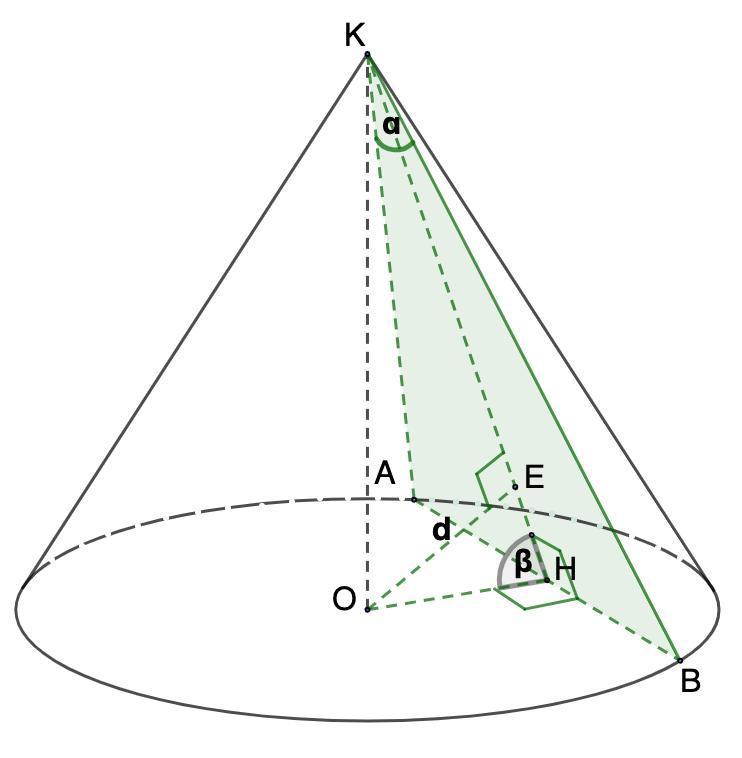
Через дві твірні конуса, кут між якими α, проведено площину, яка утворює з площиною основи кут β, відстань від центра основи конуса до площини перерізу дорівнює d.
1.Розрахуйте висоту перерізу (проведену до основи).
2.Розрахуйте довжину основи перерізу .
3.Знайдіть площу перерізу.

alinakeke11: Привет) я не знаю кто ты но у меня к тебе огромная просьба! помоги мне пожалуйста, если ты уже знаешь ответы на эти вопросы. Тогда если тебе нужна помощь в чём то другом, я попробую тоже помочь) даю слово

Morook: давай, ты в 11 класе атмосферной школы?

alinakeke11: да

alinakeke11: пожалуйста, дай мне свою почту или имя пользователя в телеграмме. что бы мы могли связаться

Morook: в телеграме номер +380961236999

Ответы

Ответ дал: natalyabryukhova

Ответ:

1. Высота сечения

$\displaystyle \bf KH=\frac{2d}{sin\;2\beta }$

2. Длина основания сечения

$\displaystyle \bf AB =\frac{4d\cdot tg\frac{\alpha }{2} }{sin\;2\beta }$

3. Площадь сечения

$\displaystyle\bf S(AKB)=\frac{4d^2\;tg\frac{\alpha }{2} }{sin^22\beta }$

Объяснение:

Через две образующие конуса, угол между которыми α, проведена плоскость, образующая с плоскостью основания угол β, расстояние от центра основания конуса до плоскости сечения равно d.

1. рассчитайте высоту сечения (проведенную к основанию).

2. рассчитайте длину основания сечения.

3. Найдите площадь сечения.

Дано: конус;

∠АКВ = α; ∠КНО = β;

ОЕ = d

Найти: КН; АВ; S(AKB)

Решение:

Расстояние от точки до плоскости - длина перпендикуляра, опущенного из данной точки на данную плоскость.

⇒ ОЕ ⊥ КН.

1. Найдем высоту сечения.

Рассмотрим ΔОЕН - прямоугольный.

ОЕ - катет, ОН - гипотенуза.

Синус угла - отношение противолежащего катета к гипотенузе.

$\displaystyle \frac{OE}{OH} =sin\;\beta \\\\\frac{d}{OH}=sin\;\beta \;\;\;\Rightarrow \;\;\;OH=\frac{d}{sin\;\beta }$

Рассмотрим ΔОКН - прямоугольный.

ОН - катет; КН - гипотенуза.

Косинус угла - отношение прилежащего катета к гипотенузе.

$\displaystyle \frac{OH}{KH} =cos\;\beta\\ \\KH=\frac{OH}{cos\;\beta } \;\;\;\Rightarrow \;\;\; KH=\frac{d}{sin\;\beta \;cos\beta } \\\\\displaystyle \bf KH=\frac{2d}{sin\;2\beta }$

2. Найдем длину основания сечения.

Рассмотрим ΔАКВ - равнобедренный.

В равнобедренном треугольнике высота, проведенная к основанию, является медианой и биссектрисой.

⇒ ∠АКН = ∠НКВ = α/2; АН = НВ

Рассмотрим ΔКНВ - прямоугольный.

Тангенс угла - отношение противолежащего катета к прилежащему.

$\displaystyle \frac{HB}{KH} =tg\frac{\alpha }{2} \\ \\HB=KH\cdot tg\frac{\alpha }{2} } \;\;\;\Rightarrow \;\;\; HB=\frac{2d\cdot tg\frac{\alpha }{2} }{sin\;2\beta } \\\\\displaystyle \bf HB=\frac{2d\cdot tg\frac{\alpha }{2} }{sin\;2\beta }$

$\displaystyle \bf AB=2 HB=\frac{4d\cdot tg\frac{\alpha }{2} }{sin\;2\beta }$

3. Найдем площадь сечения.

Площадь треугольника равна половине произведения высоты на сторону, к которой проведена эта высота.

$\displaystyle S(AKB)=\frac{1}{2}\cdot AB \cdot KH = \frac{1}{2}\cdot \frac{4d\;tg\frac{\alpha }{2} }{sin\;2\beta } \cdot \frac{2d}{sin\;2\beta } =\frac{4d^2\;tg\frac{\alpha }{2} }{sin^22\beta }$