ABCD-трапеция, CK парралельно AB, BC=6
S1=S2 Найдите среднюю линию трапеции.
Помогите пж!
Дам 25 Баллов.​

Ответ:

Средняя линия трапеции равна 12 ед.

Пошаговое объяснение:

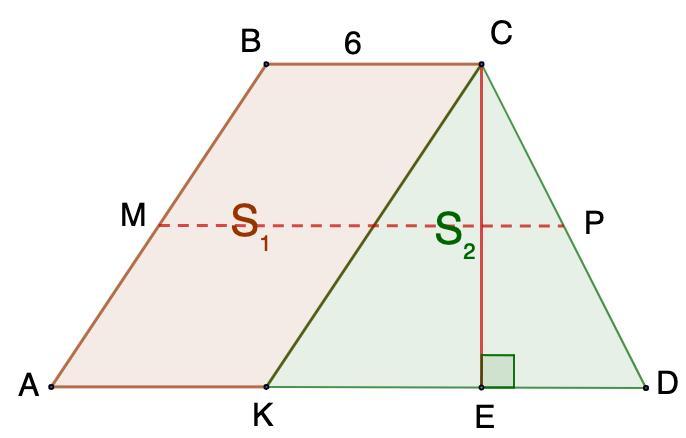
ABCD - трапеция, CK || AB, BC = 6, S₁ = S₂.

Найдите среднюю линию трапеции.

Дано: ABCD - трапеция;

CK || AB, BC = 6, S₁ = S₂.

МР - средняя линия.

Найти: МР.

Решение:

Проведем высоту СЕ.

Пусть S₁ = S₂ = S.

1. Рассмотрим АВСК.

ВС || AK (ABCD - трапеция)

CK || AB (условие)

⇒  АВСК - параллелограмм (по определению)

• Площадь параллелограмм равна произведению стороны на высоту, проведенную к этой стороне.

S₁ = AK · CE.

• Противоположные стороны параллелограмма равны.

⇒ АК = ВС = 6.

S₁ = 6 · CE.

         (1)

2. Рассмотрим ΔKCD.

• Площадь треугольника равна половине произведения стороны на высоту, проведенную к этой стороне.

Подставим CE из равенства (1)

3. Найдем МР.

• Средняя линия равна полусумме оснований.

Средняя линия трапеции равна 12 ед.

#SPJ1