Із даної точки до площини проведено дві похилі,різниця яких дорівнює 6 см. Їхні проекції на цю площину дорівнюють 27см і 15 см. Знайдіть відстань від даної точки до площини.С дано и решением пожалуйста!!!!​

Ответ:

відстань від точки до площини дорівнює 36см

Объяснение:

Дані:

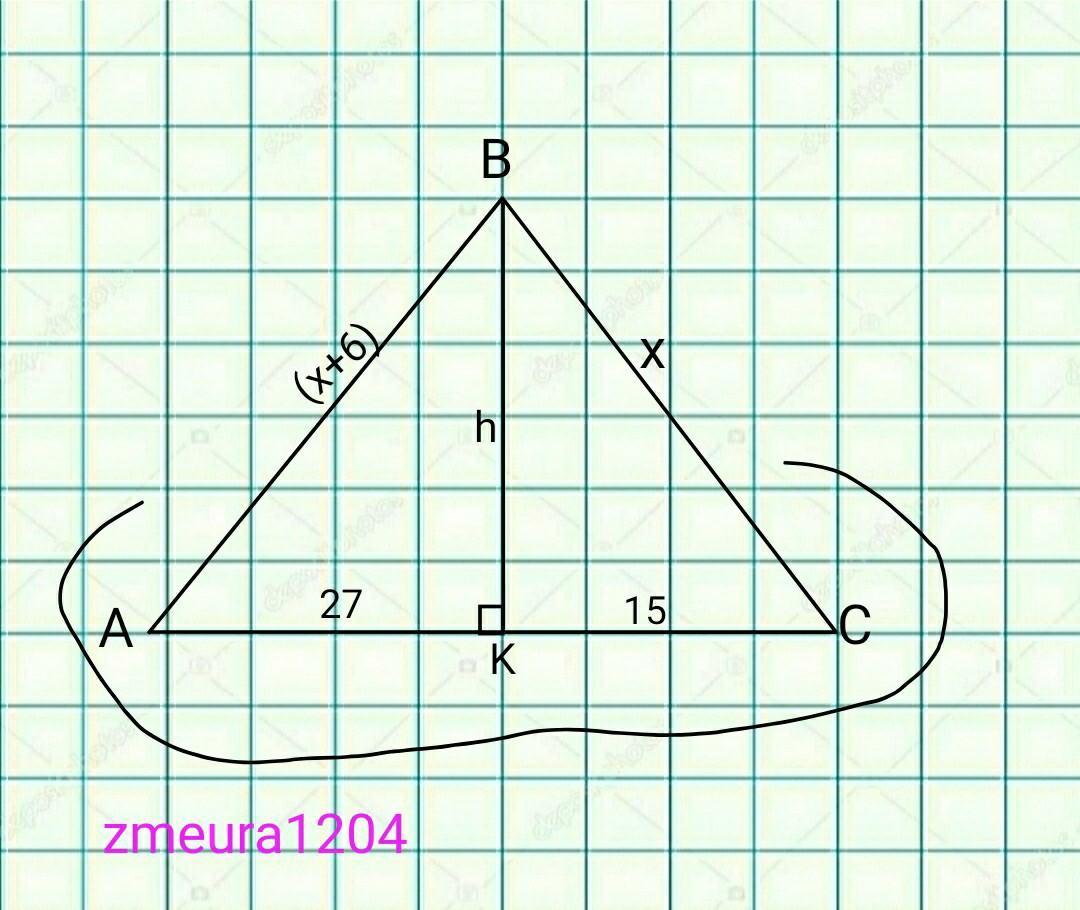
т.В не належить площині "альфа";

АВ;ВС - похилі.

АВ-ВС=6см

ВК перпендикулярно площині "альфа"

АК=27см проекція АВ

КС=15см проекція КС.

ВК=?

______

Розв'язання:

Нехай ВС буде х, тоді АВ буде (х+6).

∆ВСК- прямокутний трикутник.

За теоремою Піфагора:

ВК²=ВС²-КС²

h²=x²-15²

h²=x²-225

∆ABK- прямокутний трикутник.

За теоремою Піфагора:

ВК²=АВ²-АК²

h²=(x+6)²-27²

h²=x²+12x+36-729

h²=x²+12x-693

h²=h²

Рівняння:

х²-225=х²+12х-693

12х=693-225

12х=468. |÷12

х=39 см ВС.

ВК=√(ВС²-КС²)=√(39²-15²)=√(1521-225)=

=√1296=36см