Даю 35 балів, буду дуже вдячна

Приложения:

Ответы

Ответ дал: mathkot

Ответ:

$\boldsymbol{\boxed{ \int\limits^{1}_{0} {\bigg(x - \frac{6}{\sqrt{6x+3} } \bigg)} \, dx = 2 \sqrt{3}-5,5 }}$

10.

Площадь фигуры ограниченной линиями равна 4,5 квадратных единиц

Примечание:

По таблице интегралов:

$\boxed{\displaystyle \int x^{n} \ dx = \frac{x^{n + 1}}{n + 1} + C; n \neq -1, x > 0}$

$\boxed{ \int dx=x +C}$

По свойствам интегралов:

$\boxed{ \displaystyle \int \sum\limits_{i=1}^n {C_{i}f_{i}(x)} \, dx = \sum\limits_{i=1}^nC_{i} \int {f_{i}(x)} \, dx}$

Пошаговое объяснение:

$\displaystyle \int\limits^{1}_{0} {\bigg(x - \frac{6}{\sqrt{6x+3} } \bigg)} \, dx = \int\limits^{1}_{0} {x} \, dx - \int\limits^{1}_{0} { \frac{6}{\sqrt{6x+3} } \, dx= \frac{x^{2} }{2} \bigg|_{0}^{1} - \int\limits^{1}_{0} { \frac{d(6x+3)}{\sqrt{6x+3} } =$

$= \dfrac{1}{2 } \bigg(1^{2} - 0^{2} \bigg) - 2\sqrt{6x+3} \bigg |_{0}^{1} = 0,5(1 - 0) -2(\sqrt{6\cdot 1+3} - \sqrt{6\cdot 0+3})=$

$= 0,5 \cdot 1 -2(\sqrt{6+3} - \sqrt{0+3})= 0,5-2(\sqrt{9} - \sqrt{3})=0,5-2(3 - \sqrt{3})=$

$=0,5-6 +2 \sqrt{3}=2 \sqrt{3}-5,5$

10.

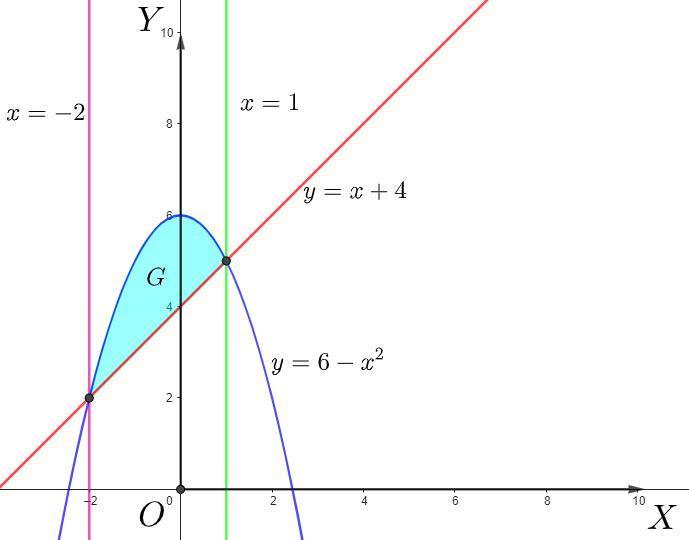
Пусть линии ограничивают область $G$ , которая имеет площадь $S$ .

Линии ограничивающие область $G$ :

$y = 6 - x^{2}$

$y = x+ 4$

Абсциссы пересечения кривых:

$6 - x^{2} = x + 4$

$x^{2} + x -2 =0$

$D = 1 - 4 \cdot 1 \cdot (-2) =1+8 = 9 = 3^{2}$

$x_{1} = \dfrac{-1+3}{2} = \dfrac{2}{2}=1$

$x_{2} = \dfrac{-1-3}{2} = \dfrac{-4}{2}=-2$

Согласно геометрическому смыслу двойного интеграла:

$\displaystyle S = \iint\limits_{G} \, dxdy = \int\limits^{1}_{-2} dx \int\limits^{6-x^{2} }_{x+4} dy = \int\limits^{1}_{-2} {y \bigg |_{x+4}^{6-x^{2} }} \, dx = \int\limits^{1}_{-2} {(6-x^{2} -(x+4))} \, dx=$

$\displaystyle = \int\limits^{1}_{-2} {(6-x^{2} -x-4)} \, dx = \int\limits^{1}_{-2} {(2-x-x^{2} )} \, dx = \int\limits^{1}_{-2} {2} \, dx - \int\limits^{1}_{-2} {x} \, dx -\int\limits^{1}_{-2} {x^{2} } \, dx=$

$\displaystyle =2\int\limits^{1}_{-2} dx - \frac{x^{2} }{2} \bigg |_{-2}^{1} - \frac{x^{3} }{3} \bigg |_{-2}^{1} = 2 \cdot x\bigg |_{-2}^{1} - \frac{1}{2} \bigg(1^{2} - (-2)^{2} \bigg) - \frac{1}{3} \bigg(1^{3} - (-2)^{3} \bigg)=$

$\displaystyle =2(1 - (-2)) - \frac{1}{2} \bigg(1 - 4 \bigg) - \frac{1}{3} \bigg(1 +8\bigg) =2(1+2) - \frac{1}{2} \cdot \bigg(-3 \bigg) - \frac{1}{3}\cdot \bigg(9\bigg)=$