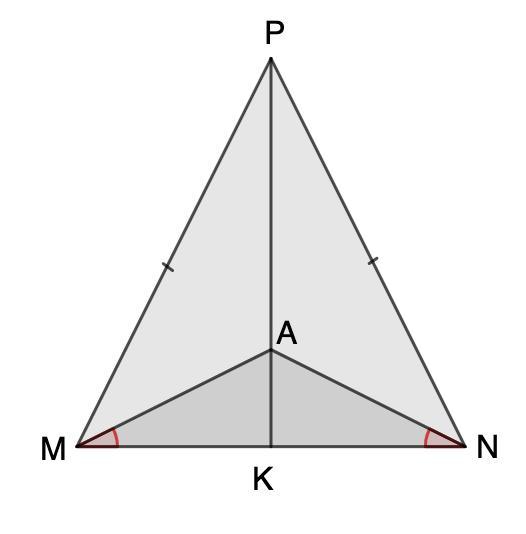
Усередині рівнобедреного трикутника МNP (PM=PN) взято точку А так, що кут AМN = куту ANM. Доведіть що промінь РА проходить через середину сторони МN

Ответ:

Доказано, что луч РА проходит через середину стороны MN.

Объяснение:

В середине равнобедренного треугольника MNP (PM=PN) взята точка А так, что ∠AMN = ∠ANM. Докажите что луч РА проходит через середину стороны MN.

Дано: ΔMNP - равнобедренный (PM=PN);

А ∈ (MNP)

∠AMN = ∠ANM

Доказать: МК = KN

Доказательство:

1. Рассмотрим ΔMAN.

∠AMN = ∠ANM (условие)

• Если в треугольнике два угла равны, то этот треугольник равнобедренный.

⇒ MA = AN

2. Рассмотрим ΔМРА и ΔAPN.

MA = AN (п.1)

PM = PN (условие)

РА - общая.

⇒ ΔМРА = ΔAPN (по трем сторонам, 3 признак)

⇒ ∠МРА = ∠АРN (соответственные элементы)

3. Рассмотрим ΔМNP  - равнобедренный.

РК - биссектриса (п.2)

• В равнобедренном треугольнике биссектриса, проведенная к основанию, является медианой.

⇒ МК = КN.

#SPJ1