1)если радиусы двух окружностей равны 3 и 5 , а расстояние между их центрами равно 1,то эти окружности пересекаются?? 2)площадь круга радиуса равен R равна 2 пR в квадрате ? 3)если вписанный угол равен 72 градуса , то центральный угол ,опирающийся на ту же дугу окружности ,равен 36 градусам? 4)если дуга окружности составляет 82 градуса ,вписанный угол ,опирающийся на эту дугу окружности ,равен 41 градусу?

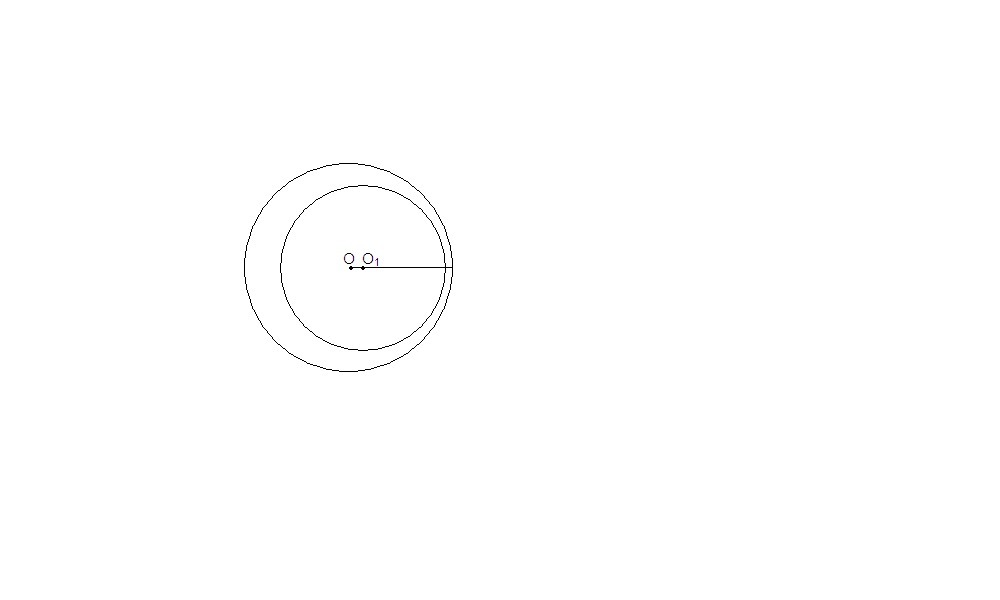
1. Окружности не пересекутся, так как расстояние между центрами меньше разности радиусов. Одна окружность будет внутри другой.
2. Площадь круга вычисляется по формуле:
     S = πR²
3. Вписанный угол равен половине центрального, опирающегося на ту же дугу. Значит центральный угол будет в два раза больше вписанного:
72° · 2 = 144°
4. Верно. Так как вписанный угол равен половине дуги, на которую опирается.