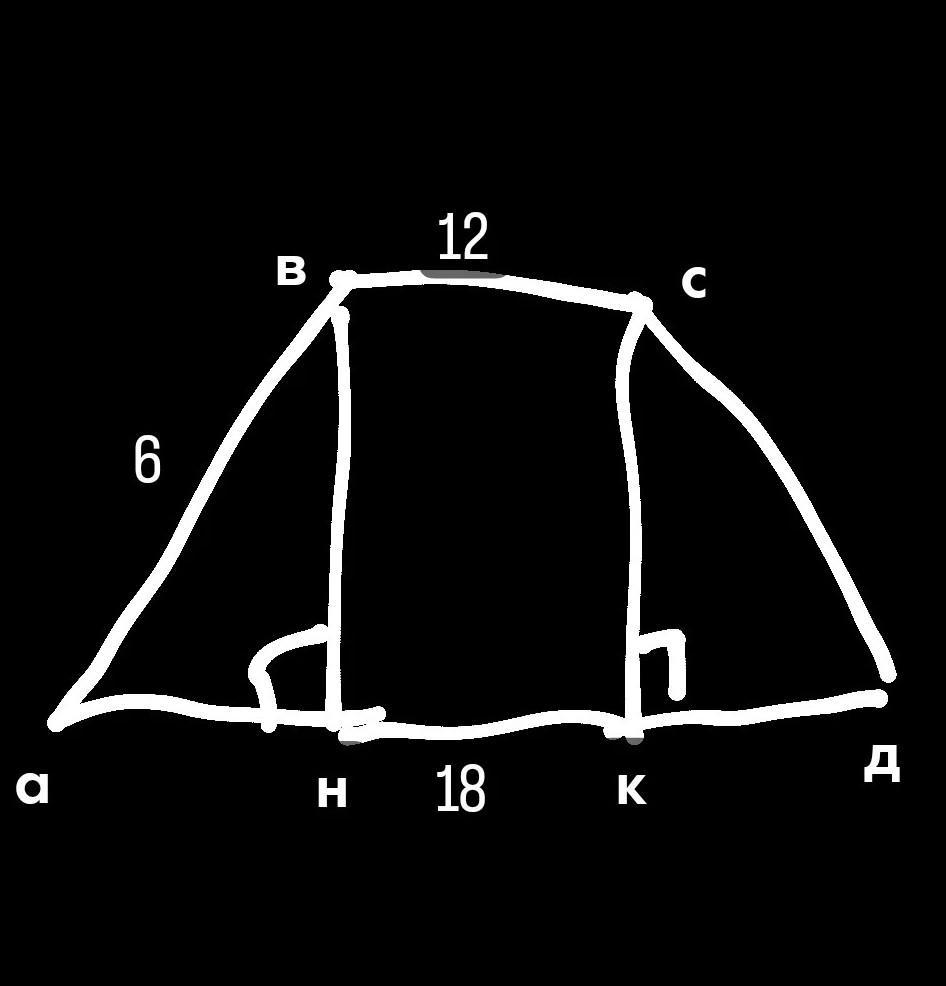
5. Найдите площадь равнобокой трапеции, если его основания 12 см и 18 см, а боковая сторона равна 6 см.​

Відповідь:

Покрокове пояснення:

Площа трапеції розраховується за формулою: Sтр = (BC+AD)/2 * h

Т.к. трапеція рівнобока і BH=CK (як висоти), то AH=DK

Тому AH = (AD-BC) / 2 = (18-12) / 2 = 3 (см)

2) За теоремою Піфагора у трикутнику ABH, знайдемо сторону ВН:

AB^2 = AH^2 + BH^2

BH^2 = AB^2 - AH^2

BH^2 = 36 - 9 = 25

BH=5 (см)

3) S = (12+18)/2 * 5 = 30/2 *5= 15*5= 75 (см^2)