С-4 ЕГЭ
Около конуса с радиусом основания R описана произвольная пирамида, у которой периметр основания равен 2p. Определить отношение объемов и отношение боковых поверхностей конуса и пирамиды.
РЕШЕНИЕ и РИСУНОК
Ответы
Пусть общая высота конуса и пирамиды равна Н.
Обозначим объемы конуса и пирамиды через V1 и V2 соответственно ,
а их боковые поверхности – через S1 и S2
тогда V1=1/3pi*R^3H , S1=pi*RL ,
где L-образующая конуса.
Найдем V2 и S2.
Так как периметр основания пирамиды равен 2р ,
а основание конуса – вписанная в основание пирамиды окружность,
то площадь основания пирамиды равна pR,
откуда V2=1/3pRH, S2=pL (высота любой грани равна L).
Тогда
V1 : V2 =1/3piR^2H : 1/3pRH = pi*R/p
S1 : S2 =pi*RL : pL = pi*R/p
Ответ V1 : V2 = S1 : S2 = pi*R/p
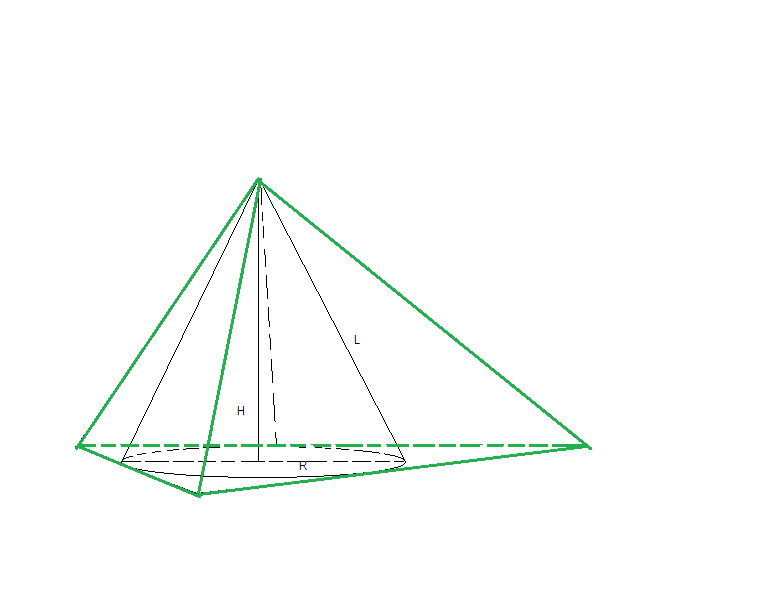
Около конуса с радиусом основания R описана произвольная пирамида, у которой периметр основания равен 2p. Определить отношение объемов и отношение боковых поверхностей конуса и пирамиды.
V1=1/3pi*R^3H , S1=pi*RL ,
L-образующая конуса.
V2=1/3pRH, S2=pL (высота любой грани равна L).
V1 : V2 =1/3piR^2H : 1/3pRH = pi*R/p
S1 : S2 =pi*RL : pL = pi*R/p
Ответ V1 : V2 = S1 : S2 = pi*R/p
