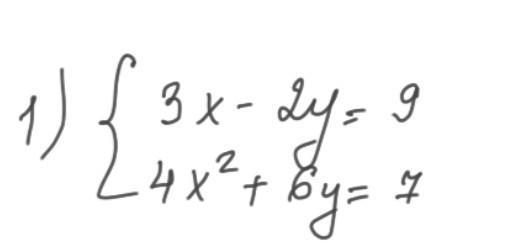Предмет: Алгебра
Автор: juli8533
Вопрос задан 1 год назад

Даю 30 б. Зробіть будь ласка з поясненнями , не просто кінцеву відповідь

Приложения:

Ответы

Ответ дал: bbbapho

Можно решить методом подстановки.

$3x - 2y = 9 , \\ 4 {x}^{2} + 6y = 7$

Из любого уравнения в системе уравнений нужно выразить одну из переменных и подставить получившееся значение этой переменной в другое уравнение. Так мы получим ещё одно значение переменной, которое подставим в изначальное уравнение и найдём все неизвестные переменные.

Итак, по порядку.

Во-первых, нужно выразить любую переменную ( $x$ или $y$ ) из любого уравнения в системе уравнений.

Для удобства лучше взять $y$ , и выразить эту переменную лучше будет из первого уравнения — оно простое.

Итак,

$3x - 2y = 9$

$- 2y = 9 - 3x$

$2y = 3x - 9$

$y = \frac{3x - 9}{2}$

Вот мы выразили значение переменной, идём дальше.

Во-вторых, нужно это значение переменной подставить в другое уравнение. Выражали из первого уравнения, подставляем во второе уравнение.

$4 {x}^{2} + 6 \times ( \frac{3x - 9}{2} ) = 7$

$4 {x}^{2} + \frac{6 \times (3x - 9)}{2 } = 7$

$4 {x}^{2} + 3 \times (3x - 9) = 7$

$4 {x}^{2} + 9x - 27 = 7$

$4 {x}^{2} + 9x - 34 = 0$

Квадратное уравнение, решу через дискриминант.

$a = 4 , \: b = 9 , \: c = - 34$

$D = {b}^{2} - 4ac = {9}^{2} - 4 \times 4 \times ( - 34) = 81 + 544 = 625$

$\sqrt{D} = \sqrt{625} = 25$ ;

$x_{1} = \frac{- b - \sqrt{D} }{2a} = \frac{-9 - 25}{8} = \frac{ - 34}{8} = - \frac{17}{4}$ ,

$x_{2} = \frac{-b + \sqrt{D} }{2a} = \frac{-9 + 25}{8} = \frac{16}{8} = 2$ .

Итак, на втором этапе мы получили два значения переменной $x$ . Эти значения нужно подставить в уравнение, которое у нас получилось на первом этапе, когда выражали переменную $y$ .

Вот в это:

$y = \frac{3x - 9}{2}$

В третьих, подставляем полученное/-ые значение/-ия переменной в исходное уравнение, с которого начинали.

Так как значений у переменной $x$ два, то и у переменной $y$ их тоже будет два.

Итак,

$x_{1} = - \frac{17}{4}$ ,

$y_{1} = \frac{3 \times ( - \frac{17}{4}) - 9}{2} = \frac{ -\frac{51}{4} - \frac{36}{4} }{2} = \frac{-\frac{87}{4} }{2} =$

тут вспоминаем правило деления на дробь: деление на дробь — это умножение на обратную ей дробь, то есть, переворачиваем ту дробь, на которую делим, и ставим знак умножения вместо деления.

$= - \frac{87}{4} \div \frac{2}{1} = - \frac{87}{4} \times \frac{1}{2} = - \frac{87}{4 \times 2} = - \frac{87}{8}$ ;

$x_{2} = 2$ ,

$y_{2} = \frac{3 \times 2 - 9 }{2} = \frac{ 6 - 9 }{2} = \frac{-3}{2} = - \frac{ 3}{2}$

Всё, нашли все значения переменных.

Важно не забывать, что если значений получилось несколько, то они записываются в паре. Например, $x_{1}$ только с $y_{1}$ , никак нельзя записывать $x_{1}$ с $y_{2}$ , это нарушение.

Ответ записывают по разному, кого как учат в школе. Либо как у меня в решении с цифрами, либо в скобках.

Ответ:

$x_{1} = -\frac{17}{4} , \: y_{1} = - \frac{87}{8}$ ;

$x_{2} = 2 , \: y_{2} = - \frac{3}{2}$

либо

Ответ:

$( - \frac{17}{4} ; \: - \frac{87}{8} ) , \: ( 2 ; \: -\frac{3}{2} )$

Можно, конечно, перевести в десятичные дроби, если вам так удобнее:

$- \frac{87}{8} = - 10.875$ ,

$-\frac{17}{4} = - 4.25$ ,

$-\frac{3}{2} = - 1.5$

Можно решить методом сложения.

$3x - 2y = 9 , \\ 4 {x}^{2} + 6y = 7$

Суть: сложить два уравнения так, чтобы исчезла одна из переменных.

Нужно, чтобы при сложении одна из переменных в сумме была равна нулю. То есть, эта самая переменная в одном уравнении должна быть со знаком плюс, во втором уравнении должна быть со знаком минус. И должна иметь одинаковое число перед собой (коэффициент). И в итоге она будет равна нулю при сложении. Но как правило, нужно привести уравнение к нужному виду. В данном случае так.

Начнём.

Во-первых, приведём к нужному виду уравнения. Возьмём первое уравнение и умножим на 3, чтобы получилось $- 6y$ в первом уравнении и $6y$ во втором уравнении.