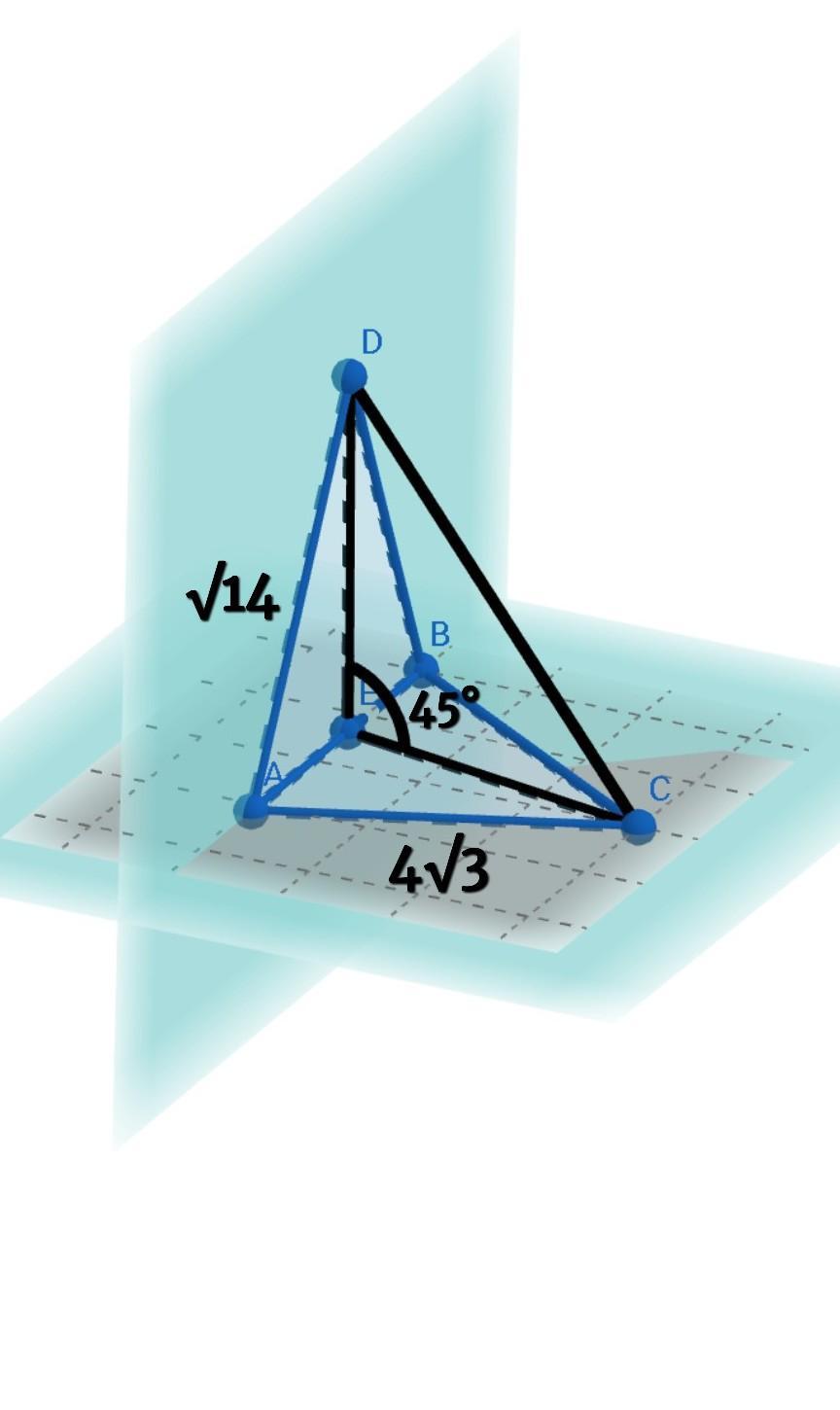
Кут між площинами трикутників ABC і ABD дорівнює 45°. Трикутник АВС - рівносторонній зі
стороною 4√3 см, трикутник ABD - рівнобедрений, AD=BD= √14 см. Знайти довжину
відрізка CD.

Ответ:

CD = √26см

Объяснение:

Угол между плоскостями треугольников ABC и ABD равен 45°. Треугольник АВС - равносторонний со стороной 4√3 см, треугольник ABD – равнобедренный, AD=BD= √14 см. Найти длину

отрезка CD.

------------------------------------------------------

Дано: (АВС), (ABD) - плоскости,∠((АВС);(ABD)) = 45°, ∆АВС - равносторонний, АС = 4√3см, ∆ABD - равнобедренный, AD = BD = √14 см

Найти: CD

⠀⠀⠀⠀⠀⠀⠀⠀Решение

• Угол между пересекающимися плоскостями определяется двугранным углом, т.е. двумя полуплоскостями с общей прямой пересечения.Градусная мера двугранного угла равна градусной мере соответствующего ему линейного угла, который является углом между перпендикулярами к ребру двугранного угла.
• Из вершин треугольников АВС и ADC опустим перпендикуляры. Угол между этими перпендикулярами и есть угол между этими плоскостями.

• Рассмотрим ∆АВС - равносторонний, и найдем его высоту(EC) по формуле: , где а - длина стороны равностороннего треугольника.

⠀⠀⠀

• Теперь рассмотрим ∆ABD - равнобедренный. Высота DE является ещё и медианой, и делит АВ на 2 равных отрезка по 2√3 см. В ∆ADE, DE согласно Т.Пифагора равна:

⠀⠀⠀⠀DE = √((√14)² - (2√3)²)

⠀⠀⠀⠀DE = √(14 - 12)

⠀⠀⠀⠀DE = √2см

• Чтобы найти отрезок CD, в ∆CDE, воспользуемся теоремой косинусов, которая гласит, что квадрат любой стороны треугольника равен сумме квадратов двух других сторон минус удвоенное произведение этих сторон на косинус угла между ними.

⠀⠀⠀CD² = CE² + DE² - 2CE * DE * cos∠DEC

⠀⠀⠀CD² = 6² + (√2)² - 2 * 6 * √2 * (√2/2)

⠀⠀⠀CD² = 38 - 12

⠀⠀⠀CD = √26см

#SPJ1