1125.Даны коорднинаты двух вершин квадрата ABCD (1; - 1,5) и B (1;2). Начертите квадрат ABCD (Рассмотрите два случая) .найдите координаты вершины C и D. Вычислите площадь и периметр квадрата квадрата ABCD.
Объясните пожалуйста как найти Периметр и площадь Даю 40 баллов​

Давайте найдём длину отрезка AB, то есть

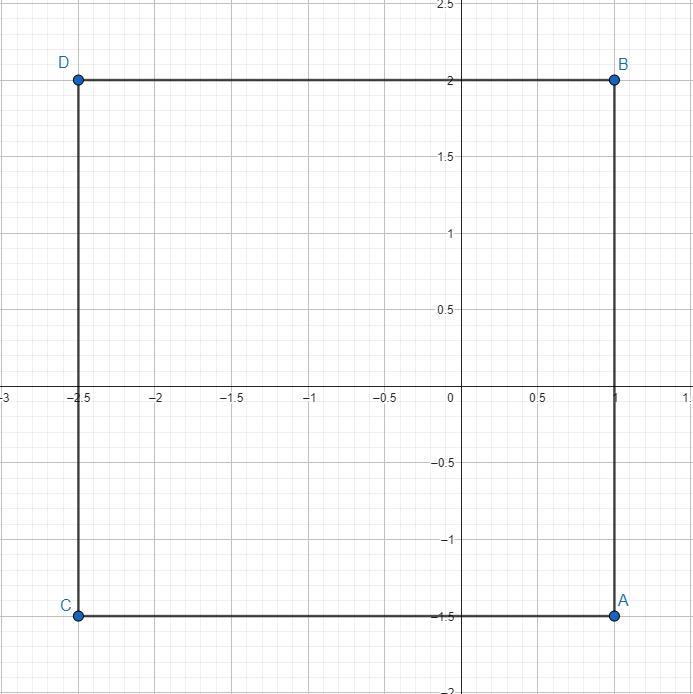
Заметим, что сторона квадрата AB пересекает ось Ox в точке 1. Так как длина стороны квадрата равна, а значит параллельная сторона стороне AB будет пересекать ось Ox  в точке . Точка A находится на координате -1,5 по оси Oy, значит точка C будет на той же координате, то есть

Точка B находится на координате 2 по оси Oy, значит точка D будет находиться на той же координате, следовательно,

Так как мы знаем длину стороны, то площадь квадрат - это произведение длины на ширину, то есть

Периметр - это сумма всех сторон, то есть