ОЧЕНЬ СРОЧНО, ПРОШУ. Угол между высотой прямоугольного треугольника, опущенной на гипотезу, и одним из катетов равен 30°.Этот катет равен 8см. Найдите гипотенузу. ​

Ответ:  16 см

Решение:

Дано:
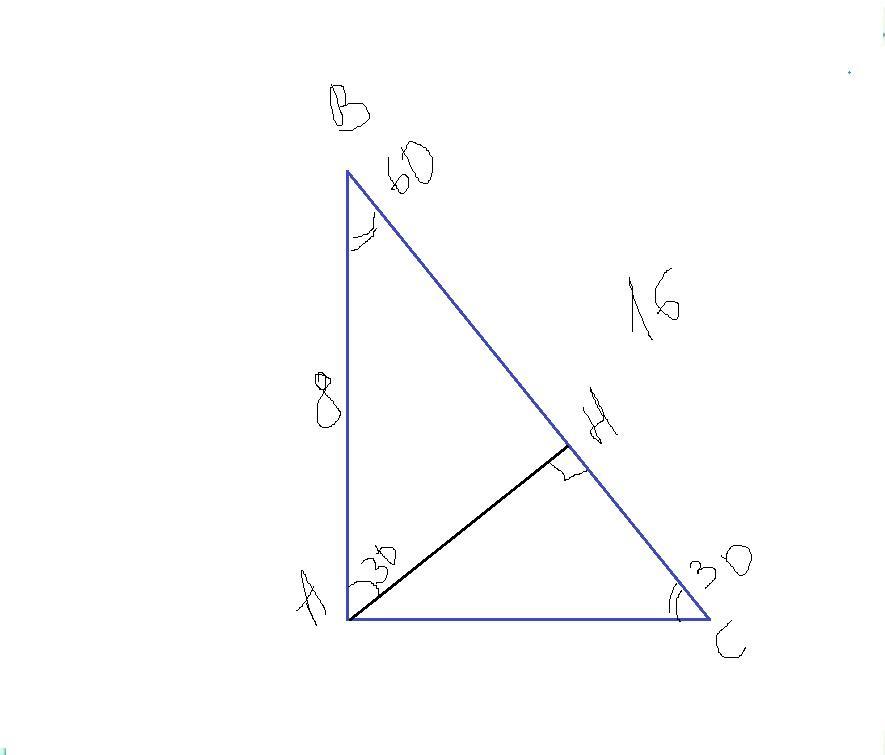
ΔАВС, ∠А=90°, АН⊥В С, ∠ВАН=30°, АВ=8 см
Найти: ВС
(Теорема (о катете, лежащем против угла в 30°). Катет прямоугольного треугольника, лежащий против угла в 30°, равен половине гипотенузы.
Отсюда гипотенуза равна удвоенной длине катета, лежащего против угла в 30°) -это теорыя
Рассмотрим ΔВНА, где∠Н=90°,∠ВАН=30°, АВ=8 см.

Согласно теореме про сумму острых углов прямоугольного треугольника ∠В+∠ВАН=90°. →∠В=90°-30°=60°.
Рассмотрим ΔАВС, где∠А=90°,∠В=60°, АВ=8 см.
∠С=90°-60°=30° ( теорема про сумму острых углов прям. тр-ка).
Значит АВ- катет, лежащий протыв угла в 30°.
АВ=1/2 ВС→ ВС=2*АВ=2* 8 см=16 см