Найди площадь круга, вписанного в правильную трапецию с основаниями длиной 6 и 12 см и периметром 36 см
dobra888:
правильної трапеції не існує в природі ( і науці ) !
Ответы
Ответ дал:
0
Відповідь:
72π см^2
Пояснення:
Оскільки периметр трапеції дорівнює 36 см, то сума її бічних сторін дорівнює:
36 - 6 - 12 = 18 см
Оскільки трапеція правильна, то її бічні сторони рівні між собою, тому кожна з них дорівнює:
18/2 = 9 см
Висота правильної трапеції може бути обчислена за теоремою Піфагора:
h = √(9^2 - 3^2) = √72 = 6√2 см
Радіус круга, вписаного в правильну трапецію, дорівнює висоті цієї трапеції. Тому площа круга дорівнює:
πr^2 = π * (6√2)^2 = 72π см^2
Отже, площа круга, вписаного в правильну трапецію з основами довжиною 6 і 12 см і периметром 36 см, дорівнює 72π см^2.
Ответ дал:
2
Ответ:
вот ответ
Объяснение:
на листочке ,2 фото
Приложения:

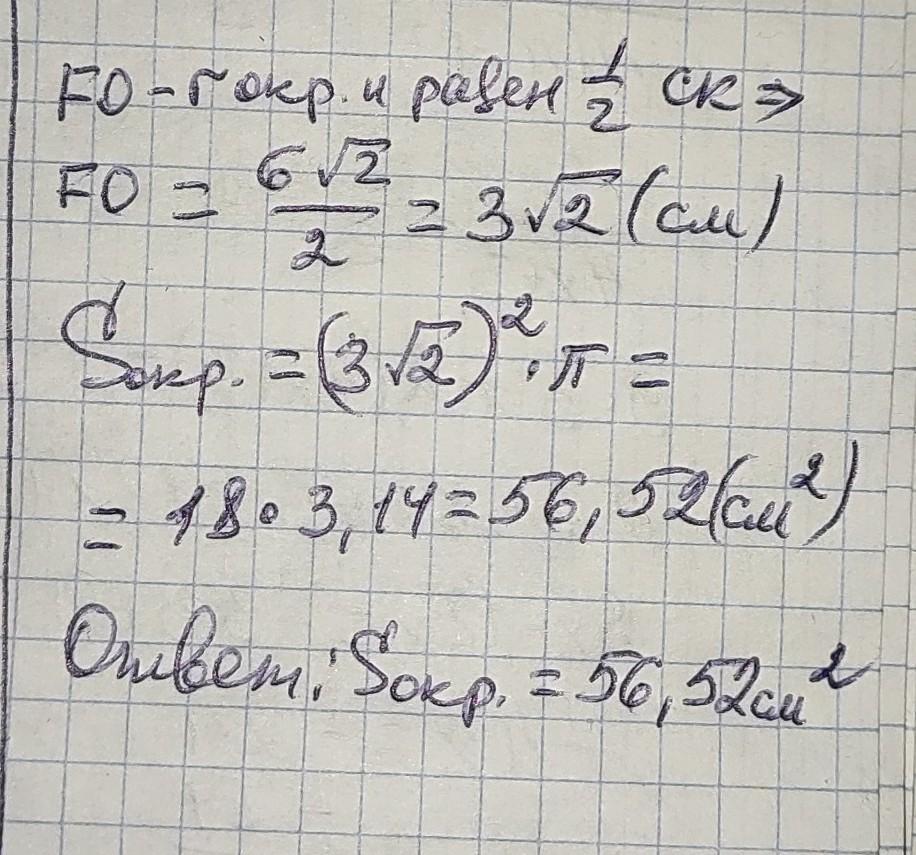
Похожие вопросы
1 год назад
1 год назад
1 год назад
2 года назад
2 года назад