Предмет: Геометрия
Автор: 250718a
Вопрос задан 1 год назад

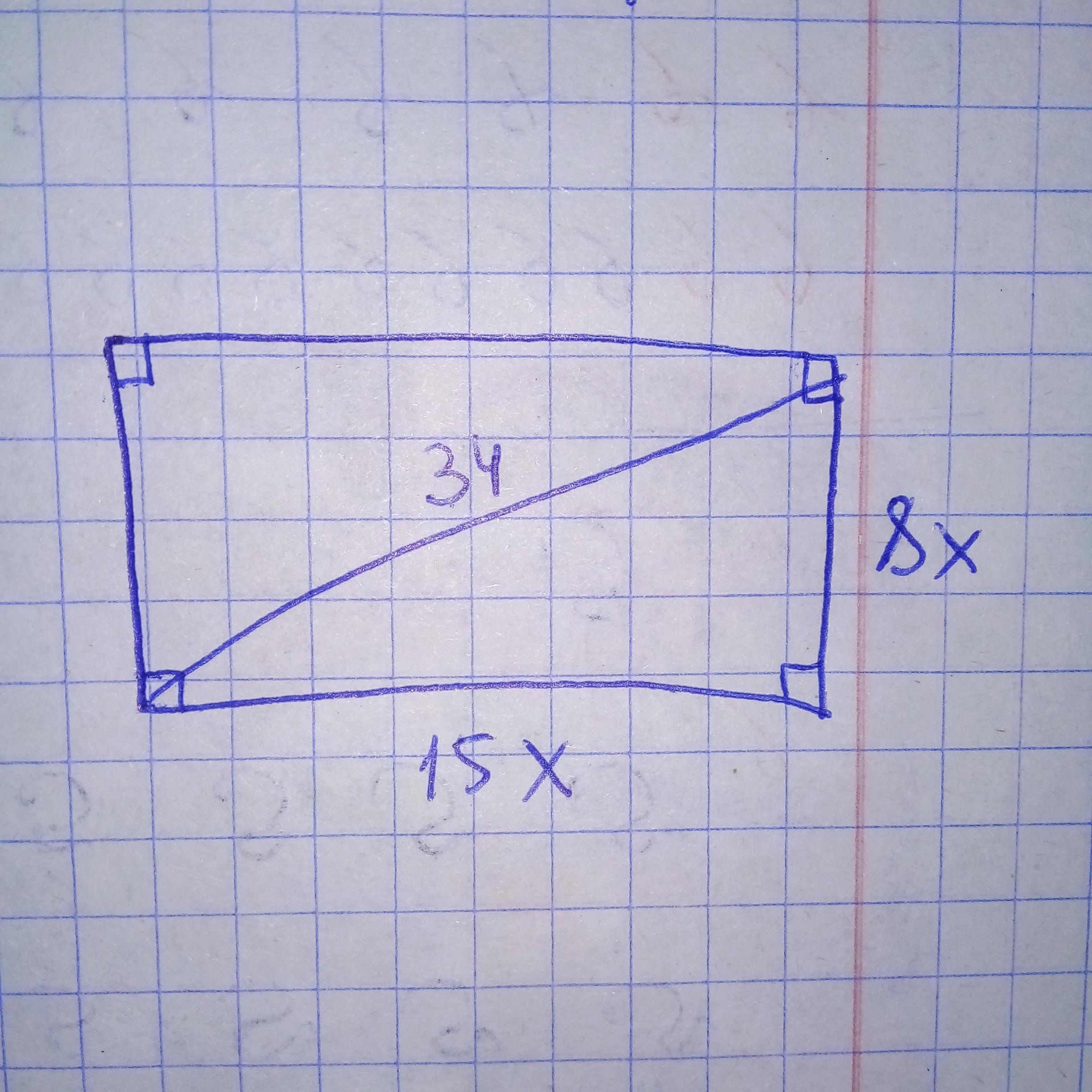
Сторони прямокутника відносяться як 8:15, а його діагональ 34 см знайти площу прямокутника. Допоможіть будь ласка терміново.

Ответы

Ответ дал: wrcon

здесь у нас есть прямоугольный треугольник, поэтому применяем теорему пифагора для нахождения икс:

${15}^{2} {x}^{2} + {8}^{2} {x}^{2} = {34}^{2} \\ 225 {x}^{2} + 64 {x}^{2} = 1156 \\ {x}^{2} (225 + 64) = 1156 \\ {x}^{2} \times 289 = 1156 \\ {x}^{2} = 1156 \div 289 = 4 \\ x = \sqrt{4} = 2$

находим стороны, подставляя найденное значения икс:

$15x = 15 \times 2 = 30см \\ 8x = 8 \times 2 = 16см$

и наконец находим площадь прямоугольника:

$S = ab = 30 \times 16 = 480 {см}^{2}$

Приложения:

Похожие вопросы

Литература

1 год назад

художні особливості червоне і чорне паспорт

История

1 год назад

Які ідеї просвітників було втілено у програмних документах декабристів

Алгебра

1 год назад

помогите решить задачу (желательно подробно)

Математика

1 год назад

пж помогите по математике даю баллов с решением

Русский язык

2 года назад

1) Вообще из всех людей, когда-либо встречавшихся с Чеховым, не было, кажется, ни одного, кто, вспоминая о нем, не отметил бы этой его глубоко народной черты: лютой ненависти к самовозвеличению и

Химия

2 года назад

Установите соответствие между уравнением реакции в молекулярном и сокращенном ионном видах. K2CO3 + 2HCl = 2KCl + H2O + CO2 CO2 + 2KOH = K2CO3 + H2O 2LiOH + H2SO4 = Li2SO4 + 2H2O NaOH +

Математика

8 лет назад

Великий прямокутник ,зображений на малюнку справа складається з дев'яти однакових прямокутників більша сторона яких дорівнює 10см .чому дорівнює периметр великого прямокутників?

Математика

8 лет назад

длина цветника прямоугольной формы равна 20 метров , а ширина 5 метров . его площадь составляет десятую часть площади огорода .найди площадь огорола . условие подалуйста , только быстро