Визначити найбільше значення функції y=x/36+x^2

на промені [0;+∞). Вказати стаціонарні точки.

Ответ:

Наибольшее значение функции: y наиб. = у(6) = 1/12.

Стационарные точки: x = ± 6

Объяснение:

Определить наибольшее значение функции

на луче [0;+∞). Указать стационарные точки.

y(0) = 0

Определим стационарные точки.

• Стационарными точками функции называются точки, в которых производная функции равна нулю.

Найдем производную, приравняем к нулю и найдем корни.

y' = 0   ⇒   36 - x² = 0

(6 - x)(6 + x) = 0

x = ± 6 - стационарные точки.

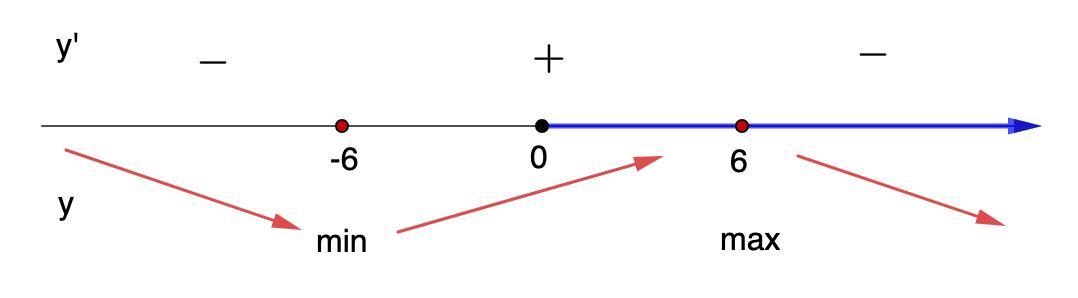
Отметим их на числовой оси и определим знаки производной на промежутках. (см. рис)

• Если "+" - функция возрастает, если "-" - функция убывает.

На данном промежутке [0; +∞):

функция возрастает на промежутке [0; 6];

функция убывает на промежутке [6; +∞).

• Если производная меняет знак с плюса на минус, то в данной точке наблюдается максимум, если с минуса на плюс, то в данной точке  - минимум.

⇒ x max = 6

y наиб. = у(6) = 1/12.

#SPJ1