ПОМОГИТЕ ПОЖАЛУЙСТА! ОТ ЭТОГО ЗАВИТИТ МОЯ ЖИЗНЬ! ПОМОГИТЕ ХОТЯБЫ ЗА ТО ЧТО НАПИСАЛА ВОПРОС ПРАВИЛЬНО)
СПАСИБО ТОМУ КТО ОТВЕТИТ, ПОМОЖЕТ!

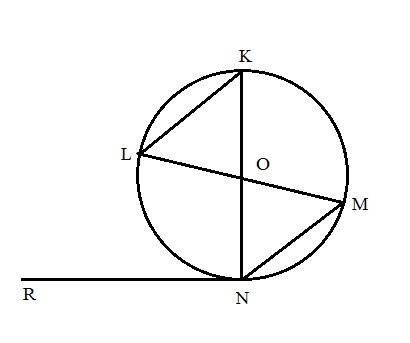
Через кінці діаметра KN проведено дві рівні хорди MN і KL.

Знайди:
Довжину діаметра KN;
Кут між хордою MN і дотичною NR, проведеною до кола в точку N;
Кут між діаметром KN і хордою KL, якщо MN=KL=5,9см;∠KNM=60°.

1. Довжина діаметра = ?см

2. Кут між хордою MN і дотичною NR: ∠MNR= ?°

3. Кут між діаметром KN і хордою KL: ∠NKL= ?°

Ответ:

Объяснение:

MN=KL=5,9см; ∠KNM=60°. Пусть центр окружности - т.О.

1. В △MON OM=ON как радиусы, => △MON - р/б, => ∠ONM=∠OMN,

∠KNM=60° => ∠OMN=60°, => ∠MON=180-2*60=60°. Таким образом, все три угла треугольника равны, значит это равносторонний треугольник и OM=ON=MN=5,9см. Диаметр KN=2*ON=2*5,9=11,8 см.

2. Радиус, проведённый в точку касания перпендикулярен касательной, значит ∠ONR=90°. ∠ONM=60°, => ∠MNR=90+60=150°.

3. Рассмотрим △MON и △LOK. У них OM=OL, ON=OK как радиусы, ∠MON=∠LOK как вертикальные. => △MON=△LOK по второму признаку. Значит △LOK также равносторонний и ∠NKL=60°.