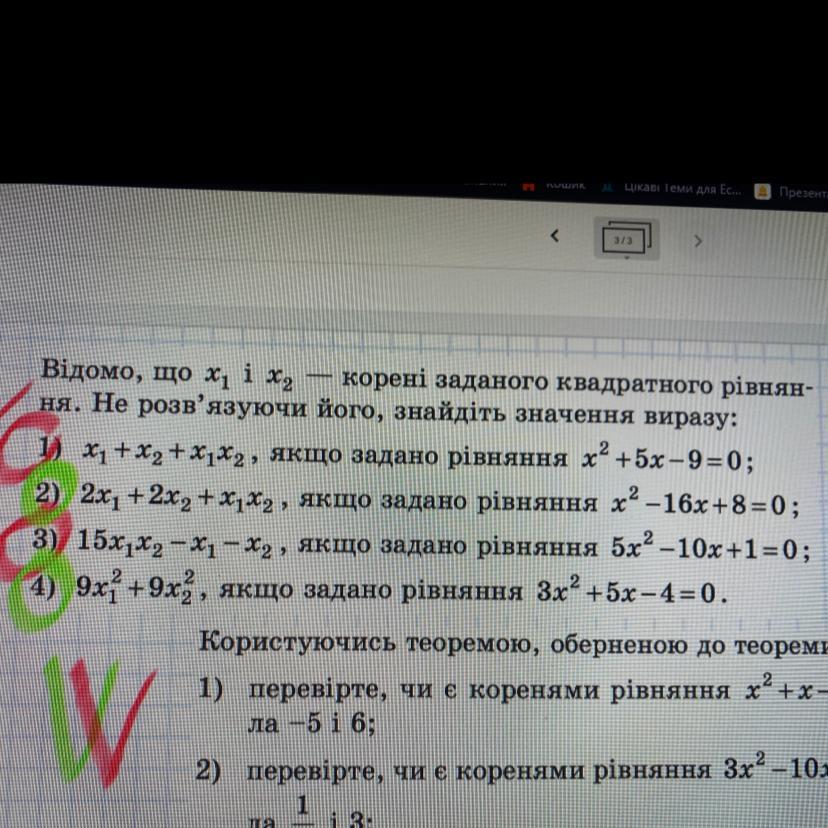
Відомо, що х1 і х2 - корені заданого квадратного рівняння. Не розв’язуючи його, знайдіть значення виразу:

Ответ:

1) x₁ + x₂ + x₁x₂ = -14

2) 2x₁ + 2x₂ + x₁х₂ = 40

3) 15x₁x₂ - x₁ - x₂ = 1

4) 9х₁² + 9х₂² = 49

Объяснение:

Известно, что х₁ и х₂ - корни заданного квадратного уравнения. Не решая его, найдите значение выражения:

1) x₁ + x₂ + x₁x₂, если задано уравнение x² + 5х - 9 = 0;

2) 2x₁ + 2x₂ + x₁х₂, если задано уравнение x² - 16х + 8 = 0;

3) 15x₁x₂ - x₁ - x₂, если задано уравнение 5х² - 10x + 1=0;

4) 9х₁² + 9х₂², если задано уравнение 3x² + 5x - 4 = 0.

• Воспользуемся теоремой Виета:

• Если x₁, x₂ - корни уравнения x²+ px + q = 0, то

             x₁ + x₂ = -p; x₁ · x₂= q

1) x₁ + x₂ + x₁x₂, если задано уравнение x² + 5х - 9 = 0;

⇒ x₁ + x₂ = -5;   x₁x₂ = -9.

x₁ + x₂ + x₁x₂ = -5 - 9 = -14

2) 2x₁ + 2x₂ + x₁х₂, если задано уравнение x² - 16х + 8 = 0;

⇒ x₁ + x₂ = 16;   x₁x₂ = 8.

2x₁ + 2x₂ + x₁х₂ = 2(х₁ + х₂) + x₁х₂ = 2 · 16 + 8 = 40

3) 15x₁x₂ - x₁ - x₂, если задано уравнение 5х² - 10x + 1=0;

Так как теорема Виета справедлива для приведенного квадратного уравнения (коэффициент при х² равен 1), разделим на 5 правую и левую части уравнения:

х² - 2х + 1/5 = 0

⇒ x₁ + x₂ = 2;   x₁x₂ = 1/5.

15x₁x₂ - x₁ - x₂ = 15x₁x₂ - (x₁ + x₂) = 15 · 1/5 - 2 = 3 - 2 = 1

4) 9х₁² + 9х₂², если задано уравнение 3x² + 5x - 4 = 0.

Разделим на 3 правую и левую части уравнения:

х² + 5/3 х - 4/3 = 0

⇒ x₁ + x₂ = -5/3;   x₁x₂ = -4/3

9х₁² + 9х₂² = 9(х₁² + х₂²)

Выражение в скобках дополним до полного квадрата. Для этого прибавим и вычтем 2x₁x₂:

9(х₁² + 2x₁x₂ + х₂² - 2x₁x₂) = 9 · ((x₁ + x₂)² - 2x₁x₂) =

#SPJ1