Из одной вершины на две стороны параллелограмма опустили высоты, длины которых равны 2 и 3,2 . Длина большей стороны параллелограмма равна 4. Найдите длину другой стороны.

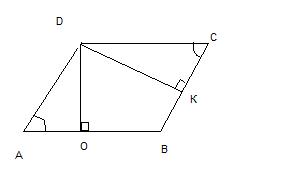
1. Построив две высоты, получаем два прямоугольных треугольника AOD и DKC. Эти треугольники подобны по первому признаку подобия (углы AOD и DKC равны по 90°, углы А и С равны как углы параллелограмма).
2. В прямоугольном треугольнике найдем КС, пользуясь теоремой Пифагора:
КС² = DC² - DK² = 4² - 3.2² = 5.76, KC = √5.76 = 2.4  
3. Из подобия треугольников следует, что
=, значит
AD = 
AD = 4*2 / 2.4 = 3.33