Ответы
Ответ дал:
0
Объяснение:
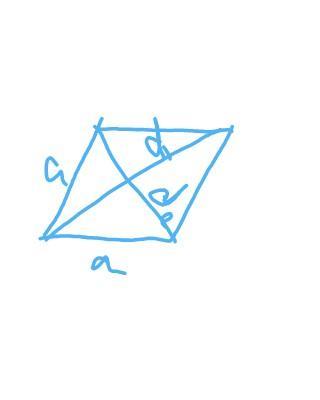
сторона а=30 см
d1-d2=12 см => d1=12+d2
диагонали ромба пересекаются под прямым углом и точкой пересечения делятся пополам.
d1=x ; d2=y
x=12+y
по теореме Пифагора:
а²=(x/2)²+(y/2)²
30²=((12+y)/2)²+(y/2)²
900=(6+0,5y)²+(0,5y)²
900=36+6y+0,25y²+0,25y²
900=36+6y+0,5y²
0,5y²+6y-864=0
D=36-4•0,5•(-864)=1764
y1=(-6-42)/2•0,5= -48 не подходит
у2=(-6+42)/1=36 см
d2=36 cм
d1=12+36=48 см
S=(d1•d2)/2=(48•36)/2=864 см²
ответ: 864 см²
Приложения:
valerij2103005:
Здравствуйте! Могу я Вас попросить, помочь мне решить задачу по геометрии? Задание у меня в профиле. Я была бы Вам очень благодарна!
Ответ дал:
0
Відповідь: 864 см²
Пояснення: розв'язання завдання додаю
Приложения:

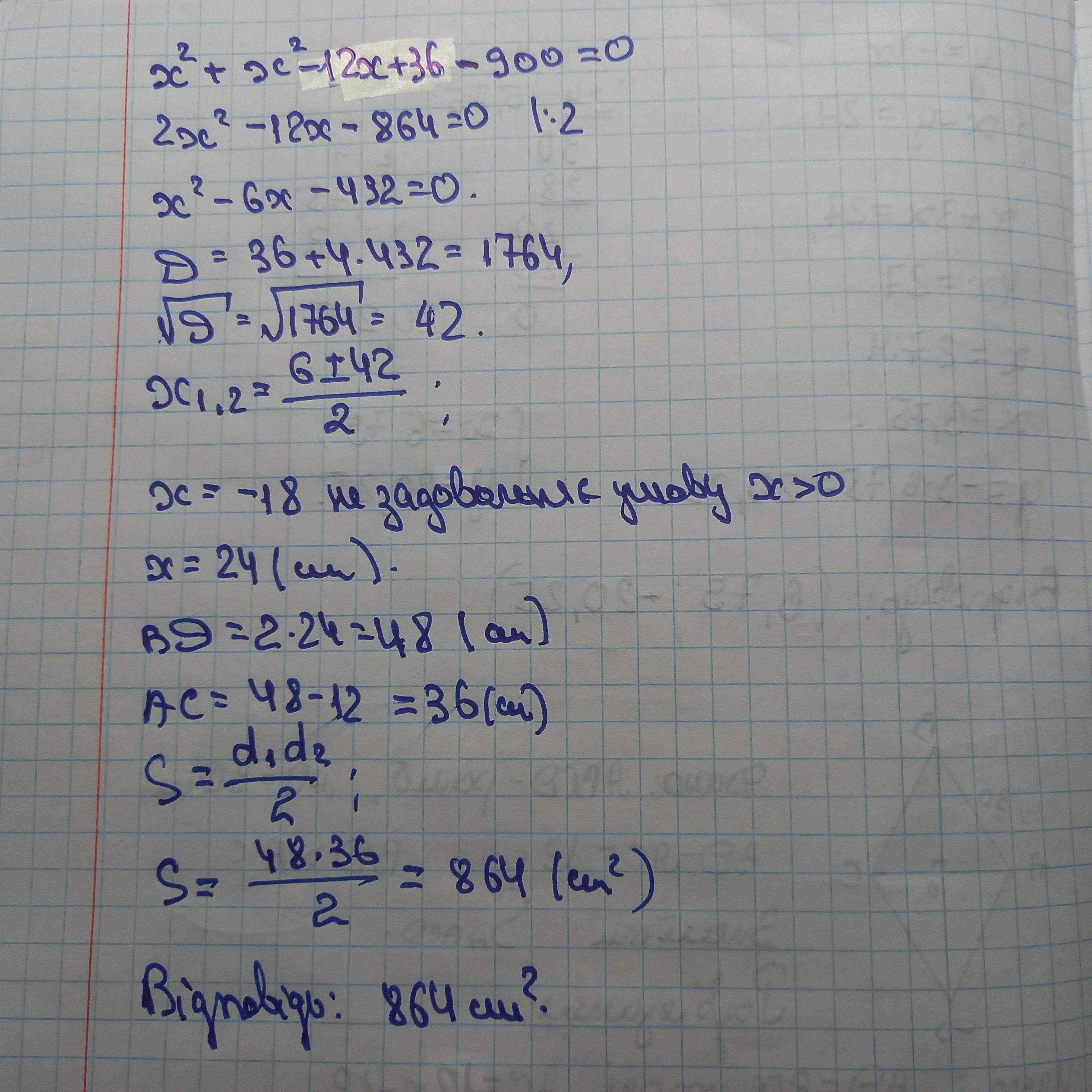
Похожие вопросы
1 год назад
1 год назад
1 год назад
1 год назад
2 года назад
2 года назад
8 лет назад
8 лет назад