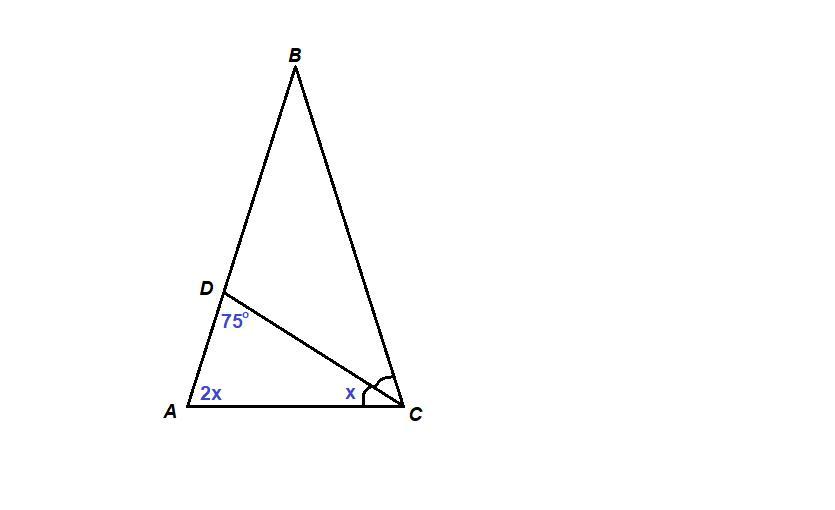
В равнобедренном треугольнике ABC с основанием AC проведена биссектриса CD. найти углы треугольника ABC, если угол ADC равен 75(градусов)

Рассмотрим треугольник ADC :
Т.к. СD-биссектриса,то угол ACD равен половине угла А (угол A=угол C , т.к. треугольник равнобедренный)
Пусть угол ACD=x,тогда
x+2x+75=180
3x=105
x=35
угол А=угол С=35*2=70
угол В=180-70*2=40

Ответ:   70°,  70°,  40°.

Объяснение:

Пусть ∠ACD = х, тогда ∠АСВ = 2х, так как CD биссектриса угла АСВ.

∠САВ = ∠АСВ = 2х как углы при основании равнобедренного треугольника.

Рассмотрим ΔACD:

Сумма углов треугольника 180°, составим уравнение

x + 2x + 75° = 180°

3x = 105°

x = 35°

∠ACB = 2 · 35° = 70°

∠CAB = ∠ACB = 70°

∠ABC = 180° - (∠CAB + ∠ACB) = 180° - 140° = 40°