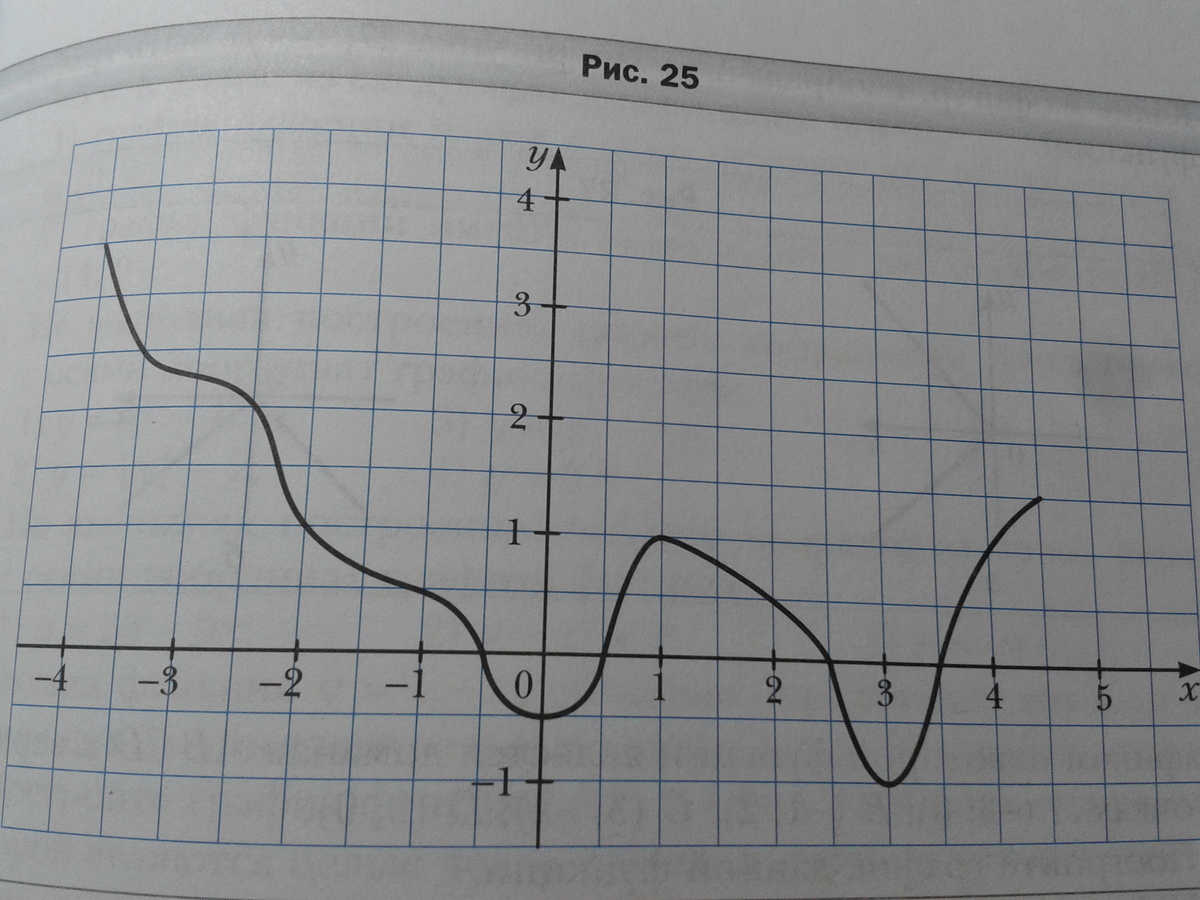
На рисунке изображен график функции y=f(x). Пользуясь графиком, найдите:
1)f(-4), f(-2,5), f(0,5) f(2)
2)значения х, при которых f(x)=2,5; f(x)=1; f(x)=0;
3)область определения и область значения функции;
4)значения аргумента, при которых значения функции положительные;
5)значения аргумента, при которых значения функции отрицательные;
ЗАРАНЕЕ БЛАГОДАРНА)
Приложения:
Ответы
Ответ дал:
0
Пользуясь графиком, найдите:
1) f(-4), f(-2,5), f(0,5) f(2) - для этого ищем значение на оси абсцисс, проецируем это значение на график и с графика проецируем на ось ординат, где и смотрим значение функции, тогда
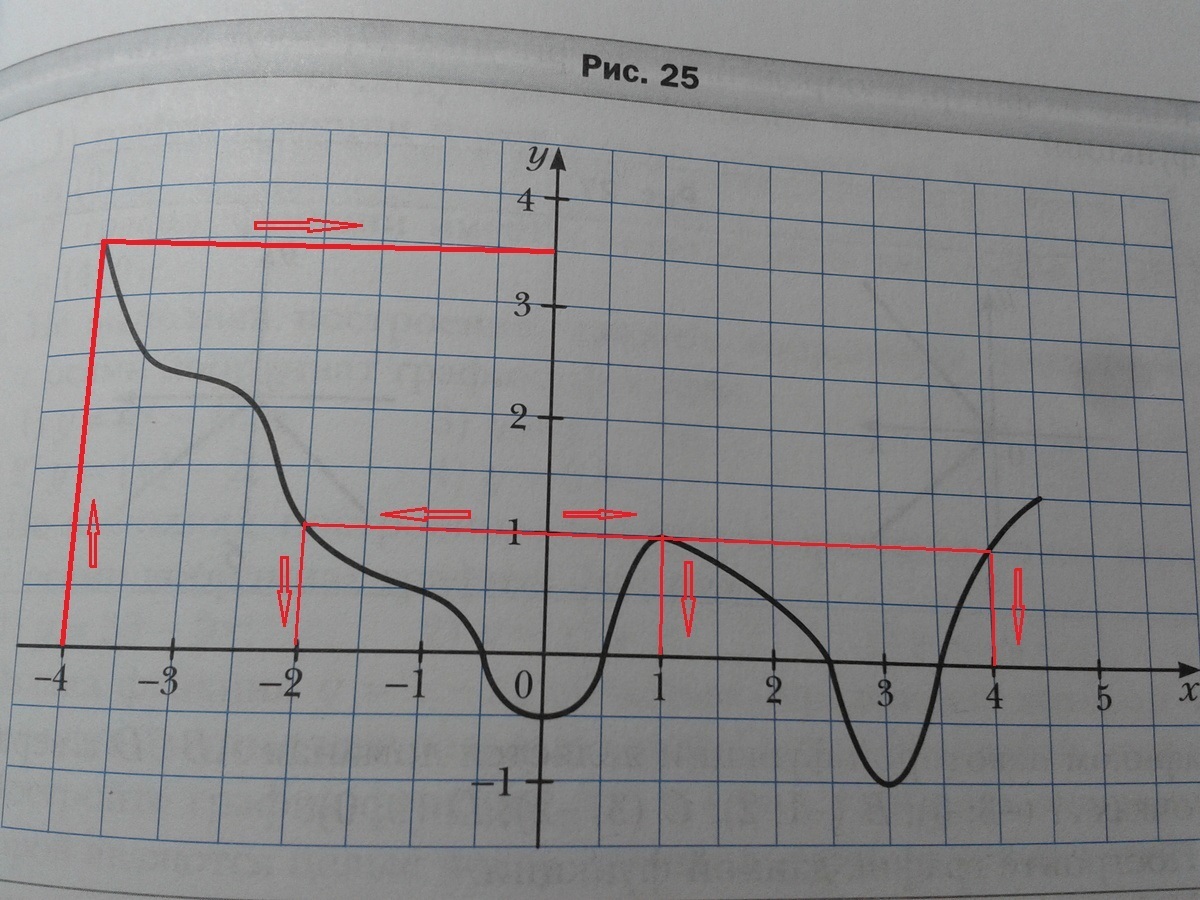
f(-4) = 3,5 (для примера смотри рисунок)
f(-2,5) = 2
f(0,5) = 0
f(2) = 0,5
2) значения х, при которых f(x)=2,5; f(x)=1; f(x)=0. Для этого ищем значение на оси ординат (Оу), проецируем это значение на график и с графика проецируем на ось абсцисс, где и смотрим значение аргумента функции, тогда
f(x)=2,5 ⇒ х = -3,5
f(x)=1 ⇒ х = -2 ; х = 1 ; х = 4 (для примера смотри рисунок)
f(x)=0 ⇒ х = -0,5 ; х = 0,5
3) область определения и область значения функции.
Тат ка функция не имеет разрыва, то она определена на всей числовой прямой от -4 до 4,5.
![x in [-4 ; 4,5 ] x in [-4 ; 4,5 ]](https://tex.z-dn.net/?f=x+in++%5B-4++%3B++4%2C5+%5D)
Область значения функции находится в интервале от -1 до 3,5. Смотри по оси ординат (Оу)
![E(y) in [-1 ; 3,5] E(y) in [-1 ; 3,5]](https://tex.z-dn.net/?f=E%28y%29+in+%5B-1++%3B++3%2C5%5D)
4) значения аргумента, при которых значения функции положительные.
![x in [-4 ; -0,5) bigcup (0,5 ; 2,5) bigcup (3,5 ; 4,5] Rightarrow f(x) textgreater 0 x in [-4 ; -0,5) bigcup (0,5 ; 2,5) bigcup (3,5 ; 4,5] Rightarrow f(x) textgreater 0](https://tex.z-dn.net/?f=x+in+%5B-4++%3B++-0%2C5%29++bigcup++%280%2C5++%3B++2%2C5%29++bigcup++%283%2C5++%3B++4%2C5%5D+Rightarrow++f%28x%29++textgreater+++0)
5) значения аргумента, при которых значения функции отрицательные

1) f(-4), f(-2,5), f(0,5) f(2) - для этого ищем значение на оси абсцисс, проецируем это значение на график и с графика проецируем на ось ординат, где и смотрим значение функции, тогда
f(-4) = 3,5 (для примера смотри рисунок)
f(-2,5) = 2
f(0,5) = 0
f(2) = 0,5
2) значения х, при которых f(x)=2,5; f(x)=1; f(x)=0. Для этого ищем значение на оси ординат (Оу), проецируем это значение на график и с графика проецируем на ось абсцисс, где и смотрим значение аргумента функции, тогда
f(x)=2,5 ⇒ х = -3,5
f(x)=1 ⇒ х = -2 ; х = 1 ; х = 4 (для примера смотри рисунок)
f(x)=0 ⇒ х = -0,5 ; х = 0,5
3) область определения и область значения функции.
Тат ка функция не имеет разрыва, то она определена на всей числовой прямой от -4 до 4,5.
Область значения функции находится в интервале от -1 до 3,5. Смотри по оси ординат (Оу)
4) значения аргумента, при которых значения функции положительные.
5) значения аргумента, при которых значения функции отрицательные
Приложения:
Похожие вопросы
2 года назад
7 лет назад
7 лет назад
10 лет назад
10 лет назад
10 лет назад