Ответы
Ответ дал:
1
Ответ:
MN = 16 см
Объяснение:
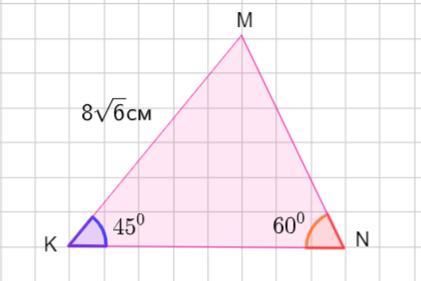
В треугольнике MNK ∠N= 60°, ∠K = 45°. Найти длину стороны MN, если MK =8√6 см.
Пусть дан ΔMNK . Воспользуемся теоремой синусов: стороны треугольника пропорциональны синусам противолежащих углов.
MN = 16 см
#SPJ1
Приложения:
Похожие вопросы
1 год назад
1 год назад
1 год назад
1 год назад
2 года назад