Предмет: Математика
Автор: mihailkvadratov
Вопрос задан 1 год назад

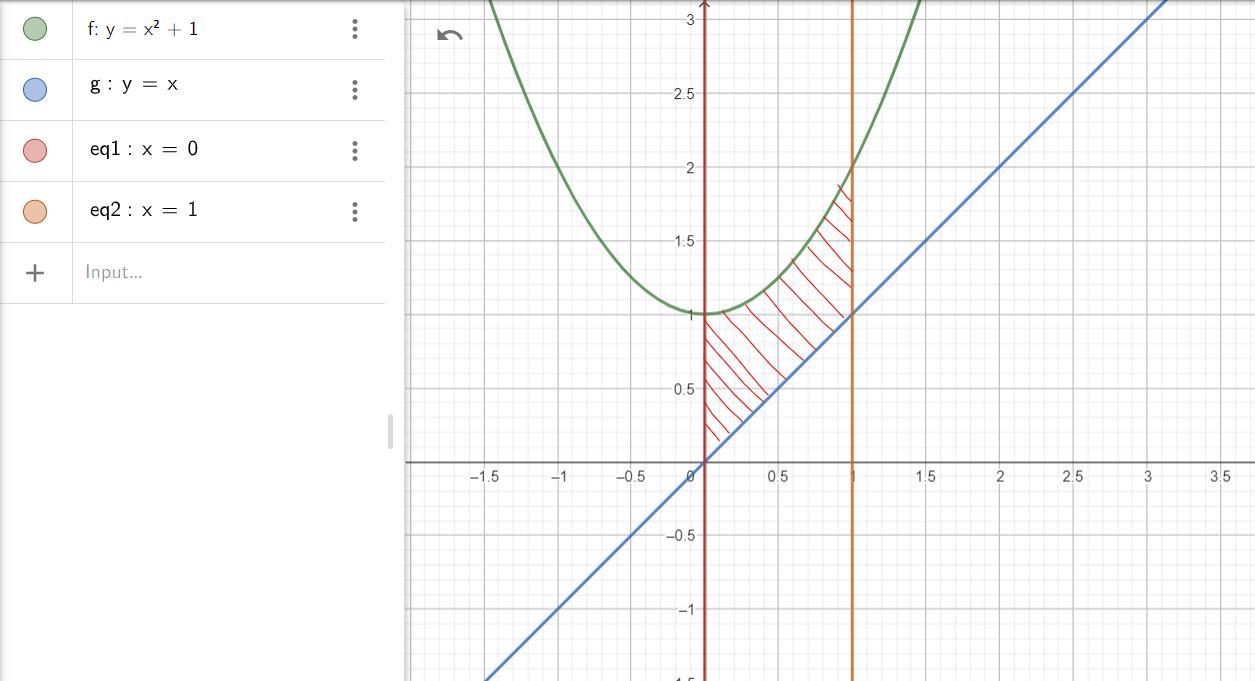
Визначити об’єм тіла, яке утворене обертанням плоскої
фігури, навколо осі Оу, обмеженої даними лініями: y=x^2 + 1, y=x, x=0, x=1

Ответы

Ответ дал: Reideen

Ответ:

Объем тела, ограниченный заданными кривыми, равен $\displaystyle \frac{5\pi}{6}$

Пошаговое объяснение:

Изобразим область, которую ограничивают графики заданных функций (см. приложение 1). Нужная нам область заштрихована красным цветом.

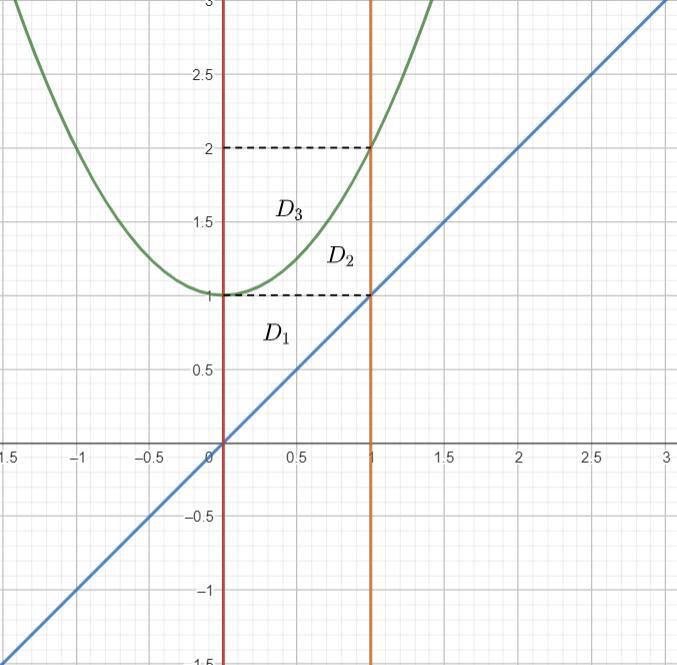
Разобьем эту область на две области D₁ и D₂ (см. приложение 2).

С областью D₁ все крайне просто: в результате вращения относительно оси Oy получится конус. Проинтегрировать не составит труда.

С областью D₂ немного сложнее: в результате вращения прямой x=1 относительно Oy у нас получится цилиндр, объем которого получается в результате вращения области D₂₃=D₂+D₃. Но по условию графики функций область D₃ не ограничивают, поэтому, чтобы получить объем тела, который ограничивает только область D₂, надо из области D₂₃ вычесть область D₃, то есть D₂=D₂₃-D₃.

Таким образом, нужная нам область равна: D=D₁+D₂=D₁+D₂₃-D₃.

Объем тела вращения относительно Oy найдем по формуле:

$\displaystyle V=\pi \int\limits^b_a {f^2(y)} \, dy$

Итак, тогда объем тела, ограниченный заданной областью, равен:

$\displaystyle V=\pi \int\limits^1_0 {y^2} \, dy+\pi \int\limits^2_1 {1^2} \, dy-\pi \int\limits^2_1 {(y-1)} \, dy=\\=\pi \bigg(\frac{y^3}{3}\bigg|^1_0 +y\bigg|^2_1-\bigg(\frac{y^2}{2} -y\bigg)\bigg|^2_1\bigg)=\\=\pi\bigg(\frac{1^3}{3} -\frac{0^3}{3} +2-1-\bigg(\bigg(\frac{2^2}{2} -2\bigg)-\bigg(\frac{1^2}{2} -1\bigg)\bigg)\bigg)=\\=\pi\bigg(\frac{1}{3} +1-\frac{1}{2}\bigg) =\boxed{\frac{5\pi}{6} }$