СРОЧНО!!!!!!
5. Бічна сторона рівнобедреного трикутника ділиться точкою дотику вписаного
кола у відношенні 5:2, рахуючи від вершини трикутника. Знайдіть сторони
трикутника, якщо його периметр дорівнює 72 см.
6. Відрізок RV — висота рівнобедреного трикутника CRM (CR=RM). На стороні
CR позначили точку F так, що FV||RM. Доведіть, що FB = FV.

Ответ:

5) Бічні сторони трикутника дорівнюють 28 см, основа 16 см

6) Довели, що FR=FV

Объяснение:

5. Бічна сторона рівнобедреного трикутника ділиться точкою дотику вписаного кола у відношенні 5:2, рахуючи від вершини трикутника. Знайдіть сторони трикутника, якщо його периметр дорівнює 72 см.

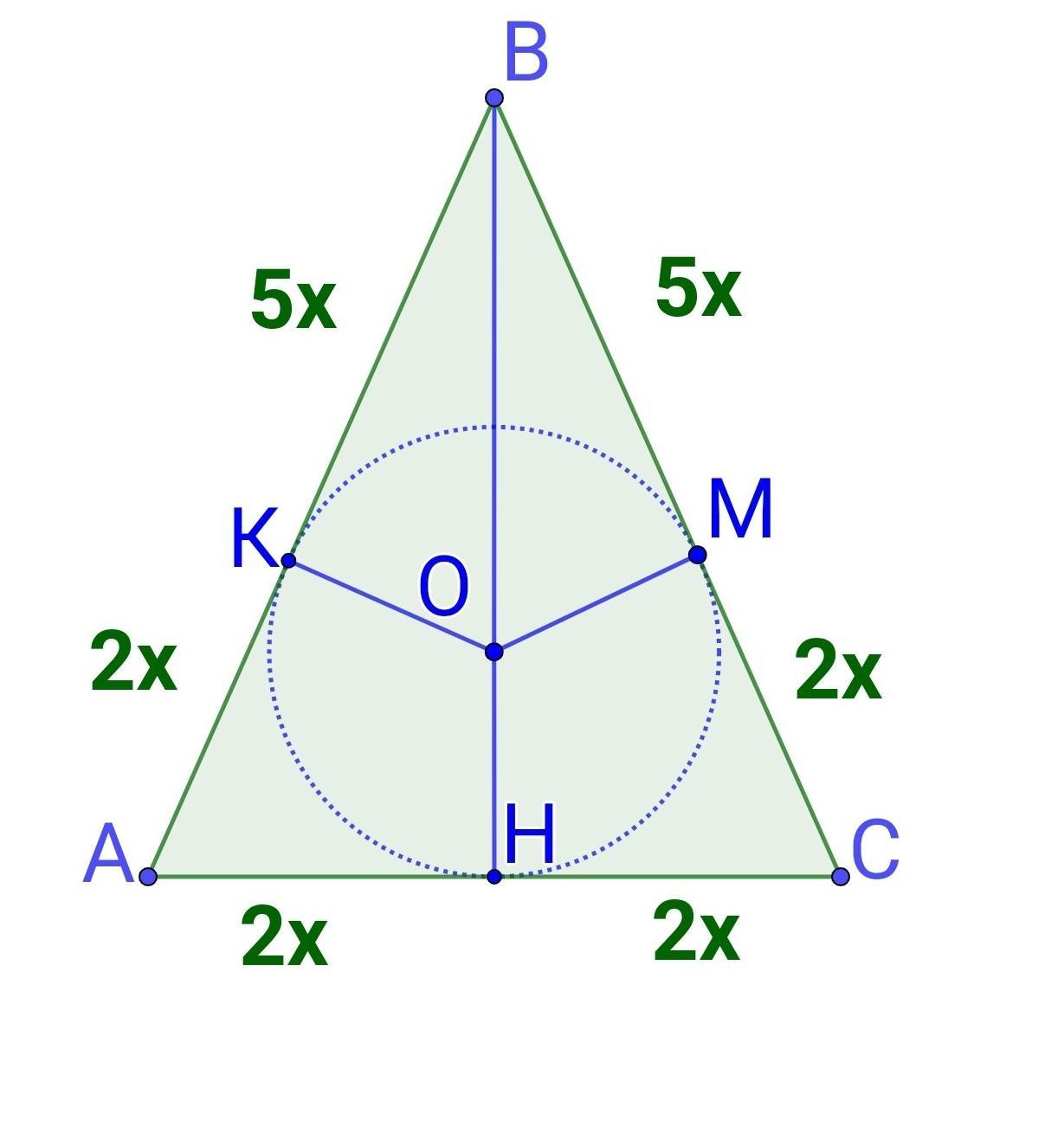
Дано: △ABC - рівнобедрений, АВ = ВС, О - центр вписаного кола, К,М,Н - точки дотику.

ВК : АК = 5 : 2, Р(АВС) = 72 см

Знайти: АВ, ВС, АС

РОЗВ'ЯЗАННЯ

За умовою ВК : АК = 5 : 2, позначимо ВК=5х, АК=2х, де х - коефіцієнт пропорційності.

За властивістю дотичних до кола, проведених з однієї точки, маємо:

ВМ=ВК=5х (см), АН=АК = 2х (см).

За аксиомою вимірювання відрізків отримаємо:

АВ=ВК+АК=5х+2х=7х (см)

ВС=АВ=7х (см).

Н - середина відрізка АС, НС=АН=2х (см).

АС=АН+НС=2х+2х=4х (см).

Р(АВС) = АВ+ВС+АС=7х+7х+4х.

18х=72

х=4

Отже АВ=ВС=7•4= 28 (см), АС =4•4= 16(см).

6. Уточнена умова:

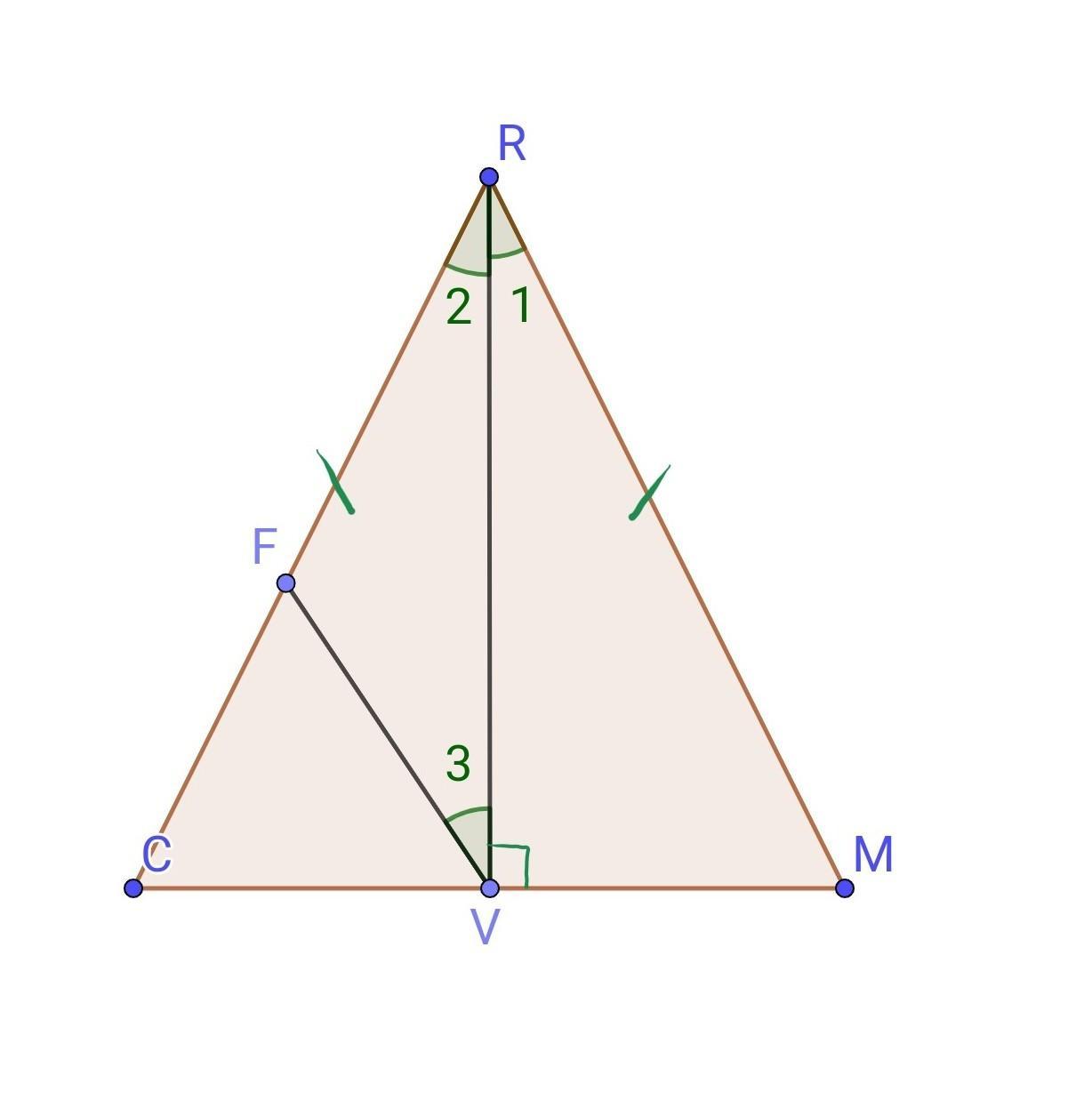
Відрізок RV — висота рівнобедреного трикутника CRM (CR=RM). На стороні CR позначили точку F так, що FV||RM. Доведіть, що FR = FV.

Дано: △CRM, CR=RM, RV⟂CM, F ∈ CR, FV || RM.

Довести: FR=FV.

Доведення

Позначимо ∠VRM за ∠1, ∠VRC за ∠2

Так як в рівнобедреному трикутнику висота буде також бісектрисою, то:

∠1=∠2.

∠1=∠3 - як внутрішні різносторонні кути при перетині паралельних прямих FV і RM січною RV.

Отже ∠2=∠3, тому △VFR - рівнобедрений з основою RV.

Тому FR=FV - як бічні сторони рівнобедреного трикутника.

Що і треба було довести.

#SPJ1