Знайдіть значення sin beta якщо cos beta = 1/3

Приложения:

Ответы

Ответ дал: tamaranedzumi

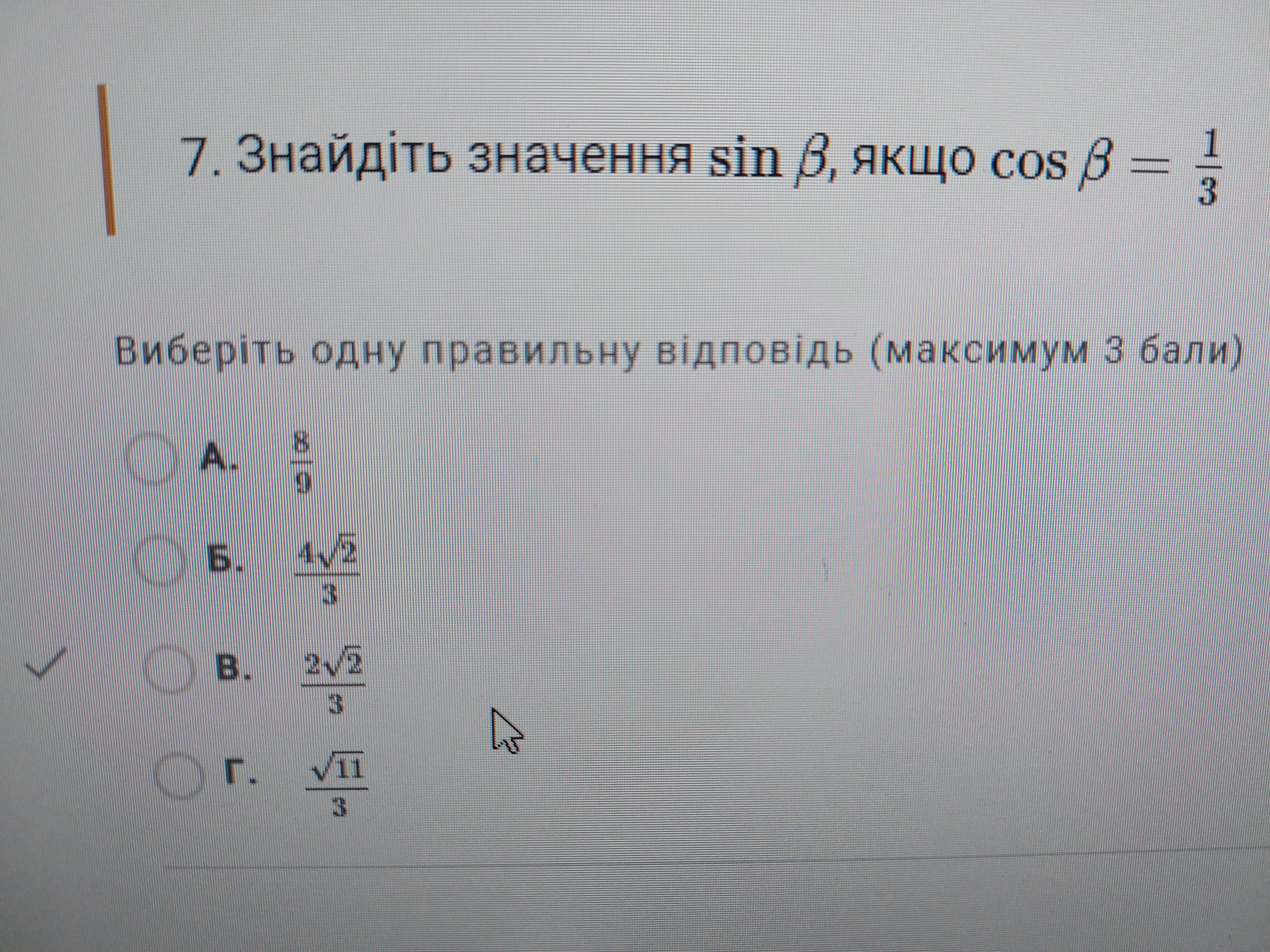
Вспоминаем основное тригонометрическое тождество

$sin^2\alpha +cos^2\alpha =1$

Отсюда выразим синус

$sin\alpha =\sqrt{1-cos^2\alpha } \\$

По условию $cos\alpha =\frac{1}{3}$ , тогда

$sin\alpha =\sqrt{1-(\frac{1}{3} )^2} =\sqrt{1-\frac{1}{9} } =\sqrt{\frac{9}{9}-\frac{1}{9} } =\sqrt{\frac{8}{9} } =\sqrt{\frac{2^2*2}{3^2} } =\frac{2\sqrt{2} }{3}$

Ответ: B

Похожие вопросы

Право

1 год назад

складіть таблицю порівняльна характеристика правового статусу іноземців і біженців

Литература

1 год назад

1. Укажи, до якого твору Горація можна дібрати іншу назву, наприклад, «Пам’ятник» Виберіть одну відповідь: «До Мельпомени» «Римській державі» «До Аполлона» «До Манлія Торквата» 2. Продовж.

Литература

1 год назад

сообщение на тему обломов и пшеницина

Физика

1 год назад

1.кутова швидкість обертання лопатей повітряного гвинта літака 14 π рад./с. , визначте скільки обертів здійснив гвинт за 8 с. 2.обчисліть доцентрове прискорення обертання тигра,який сидить біля

Английский язык

2 года назад

Поможіть дам 50 балів

История

2 года назад

що сприяло об'єднанню Німеччини у 1990р? ТЕРМІНОВО!!!!

Математика

8 лет назад

Помогите,плиз.РЕШИТЕ ЧЕРЕЗ ДИСКРИМИНАНТ: 1)5/6х-4/9х=1/3х-5 1/2 2)1/30х^2-1/15х=3/10х+19 3)(0,3m+2)^2-2m=0,8m-3 4)5/4х-3/8х=х/2-9 5)3m^2-4/8-2m+3/12=m/3-1/4 6)4y^2+5/15-2/5y=5-2y/10-1/3

Математика

8 лет назад

сделать схематический рисунок и вычислить 2:2 4:2 6:2 8:2 10:2 ... как?