Предмет: Алгебра
Автор: KSashka2005
Вопрос задан 1 год назад

< >

Решите задачу пожалуйста

Приложения:

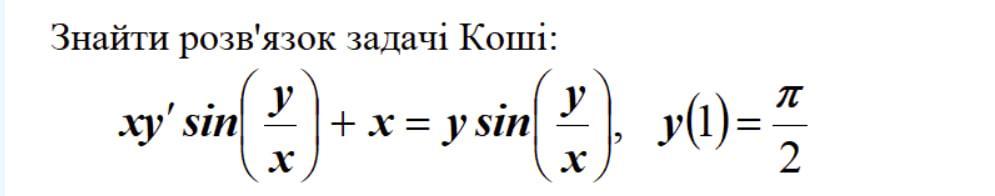
Аноним: Привіт, напиши мені в інсту, кину відповідь, andriicoval

Ответы

Ответ дал: NNNLLL54

0

Ответ:

Дифференциальное уравнение с однородными функциями .

$\bf \displaystyle xy'\, sin\frac{y}{x}+x=y\, sin\frac{y}{x}\ \ ,\ \ \ \ y(1)=\frac{\pi }{2}\\\\\\y'=\frac{y}{x}-\frac{1}{sin\dfrac{y}{x}}\ \ ,\ \ \ \ zamena:\ \ t=\frac{y}{x}\ \ ,\ \ y=tx] ] ,\ \ y'=t'x+t\\\\\\t'x+t =t-\frac{1}{sin\, t}\ \ ,\ \ \ t'x=\frac{1}{sin\, t}\ \ ,\ \ \ \ \frac{dt}{dx}\cdot x=\frac{1}{sin\, t}\ \ ,\\\\\\\int sin\, t\, dt=\int \frac{dx}{x}\ \ \ ,\ \ \ -cos\, t=ln|\, x\, |+C\ \ ,\\\\\\\boxed{\bf \ cos\, \frac{y}{x}=-ln|\, x\, |-C\ }$

Нашли общий интеграл .

Теперь найдём частный интеграл, воспользовавшись начальными условиями .

$\bf \displaystyle y(1)=\frac{\pi }{2}\ \ \Rightarrow \ \ \ cos\frac{\pi }{2}=-ln1-C\ \ ,\ \ C=0\\\\\\\boxed{\bf \ cos\frac{y}{x}=-ln|\, x\, |\ }$

Приложения:

Похожие вопросы

Английский язык

1 год назад

3 1.40 Study the key phrases. Then listen to the conversation again and answer the questions. KEY PHRASES O Talking about an event Why didn't you go to ...? How was it? I had a great time. Were there

Обществознание

1 год назад

1. Какая наука изучает общество? 2. Что такое социальный институт? 3. К какому социальному институту относятся религия, образование, СМИ, наука, культура? 4. Объясните, как на практике работают

Химия

1 год назад

робочому зошиті скласти рівняння реакції приєднання (гідрогенгалогенування, гідратації) для бутин-1-ину, пент-2-ену.

Математика

1 год назад

срочно!!! пожалуйста помогите дам 15 баллов

Математика

2 года назад

знайти кути трикутника вершинами якого є точки A(8;0;6) B(8;-4;6) C(6;-2;5)

Алгебра

2 года назад

Площадь боковой поверхности цилиндра равна 60π м2, а диаметр основания 10 м. Найдите длину образующей цилиндра.

Математика

8 лет назад

помогите решить пример столбиками пожалуйста 1,25:(10-9,82)-1:2,5=

Математика

8 лет назад

В каком классе меньше всего выбрали волка?