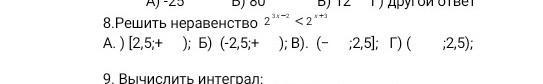помогите пожалуйста ​

Почнемо з перетворення правої частини нерівності:

2^3x-2 < 2^x+3

2^3x-2 < 2^3 * 2^x

2^3x-2 < 8 * 2^x

2^3x-2 < 2^3 * 2^x

2^3x-2 < 2^3+x

Тепер можемо записати остаточну нерівність:

2^3x-2 < 2^3+x

Щоб вирішити цю нерівність, виконаємо наступні дії:

2^3x-2 < 2^3+x

2^3x-2 < 2^3 * 2^0 * 2^x

2^3x-2 < 2^3 * 2^(x-1)

2^3x-2 < 8 * 2^(x-1)

Розділимо обидві частини на 2^(x-1):

2^3x-2 / 2^(x-1) < 8

2^(3x-x+1) < 8

2^2x+1 < 8

2^2x < 4

2^x < 2

Тут ми застосували правило простішої нерівності до того, що 2^(x-1) > 0. Оскільки 2^x < 2, ми можемо записати:

x < 1

Однак ми повинні врахувати обмеження на x, що випливає з правої частини оригінальної нерівності, тобто x повинен бути більшим за -3. Отже, остаточна відповідь:

-3 < x < 1.