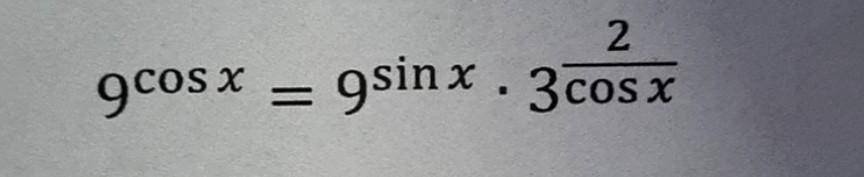100 баллов аааааааааа

Приложения:

Ответы

Ответ дал: Simba2017

ОДЗ: cos(x)≠0

x≠pi/2+pin;n∈N

все к степени тройки

3^(2cos(x))=3^(2sin(x)+2/cos(x))

приравниваю степени, так как основания одинаковы

2cos(x)=2sin(x)+2/cos(x)

домножу все на cos(x)/2

cos^2(x)=sin(x)cos(x)+1

0=1-сos^2(x)+sin(x)*cos(x)

0=sin^2(x)+sin(x)*cos(x)

sin(x)(sin(x)+cos(x))=0

1)sin(x)=0;x1=pim; m∈Z

2)sin(x)+cos(x)=0

делю все на cos(x)

tg(x)+1=0

tg(x)=-1

x2=-pi/4+pik; k∈Z

оба корня по ОДЗ подходят

matilda17562: x≠ π/2+πn; n∈N (?)

Ответ дал: сок111213

$\cos x \neq 0 \\x\neq \frac{\pi}{2} +\pi n \:, \: n \in Z\\9^{\cos x}=9^{\sin x}\times 3^{\frac{2}{\cos x }}\\3^{2\cos x}=3^{2\sin x}\times 3^{\frac{2}{\cos x }}\\3^{2\cos x}= 3^{2\sin x +\frac{2}{\cos x }}\\3^{2\cos x}= 3^{\frac{2\sin x\cos x+2}{\cos x }}\\2\cos x = \frac{2\sin x \cos x+2}{\cos x } \\2\cos^{2}x=2\sin x\cos x+2\\\cos^{2}x-\sin x\cos x-1=0\\-\sin^{2}x-\sin x\cos x=0\\\sin x (\sin x + \cos x)=0\\$

$1) \: sin x = 0\\x_{1} = \pi n \:, \: n \in Z\\ \\2) \: \sin x + \cos x =0 \: \: \: |:\cos x\\\frac{\sin x}{\cos x} +\frac{\cos x}{\cos x} =0\\ \tan x +1 =0 \\ \tan x = -1\\ x_{2} = -\frac{\pi}{4}+\pi n \: , \: n \in Z$