¡СРОЧНО!
вычислить площадь фигуры ограниченной линиями y=x^2 + 1; y=0; x=-1; x=2

Ответ:         6 кв.ед.

Объяснение:

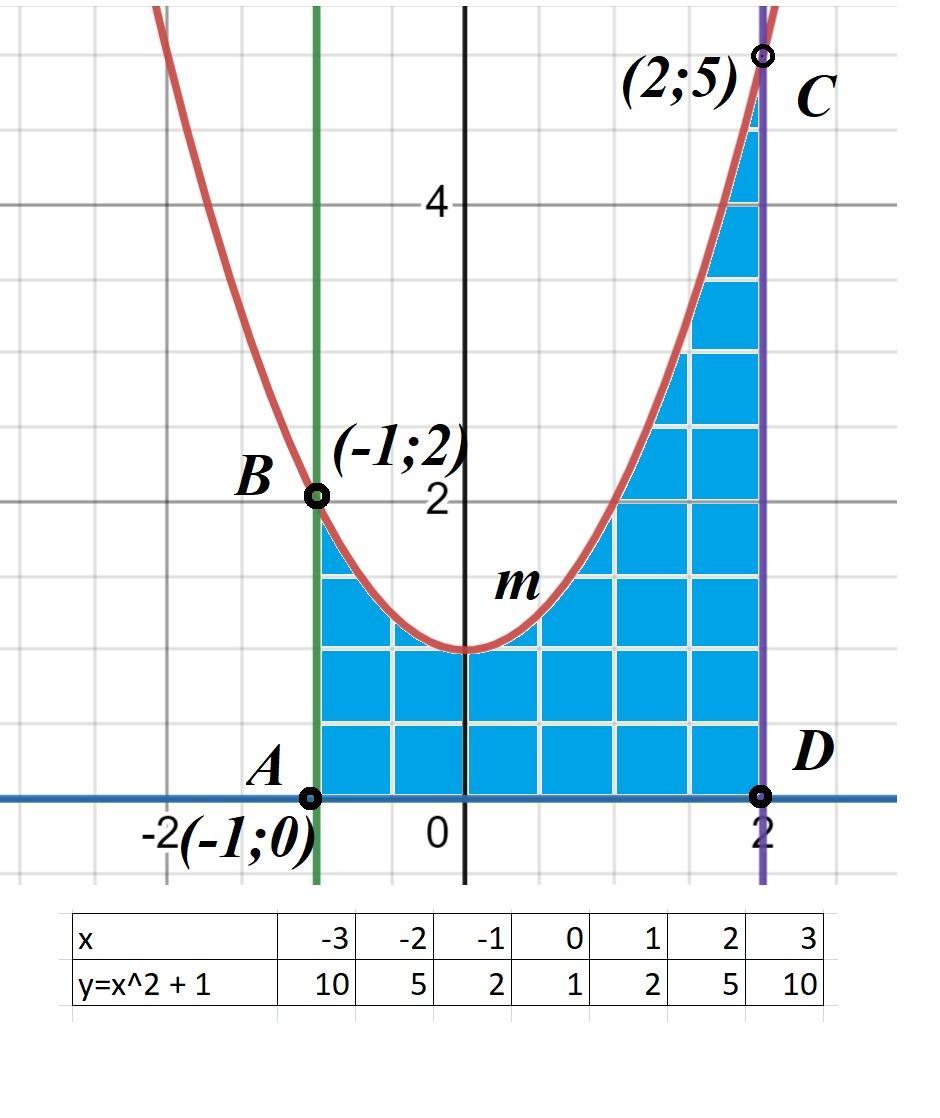
Строим графики функций y=x^2 + 1;  y=0;  x=-1;  x=2.

Площадь S(ABmCD) = ∫ₐᵇf(x)dx.

Пределы интегрирования a=-1;  b=2. (См. скриншот).  Тогда

S(ABmCD) =∫₋₁²(x^2 + 1)dx = ∫₋₁²(x²)dx +∫₋₁²(1)dx = 1/3(x³)|₋₁²+(x)|₋₁² =

= 1/3(2³-(-1)³) + (2-(-1)) = 1/3 *9 + 3 = 3+3=6 кв.ед.