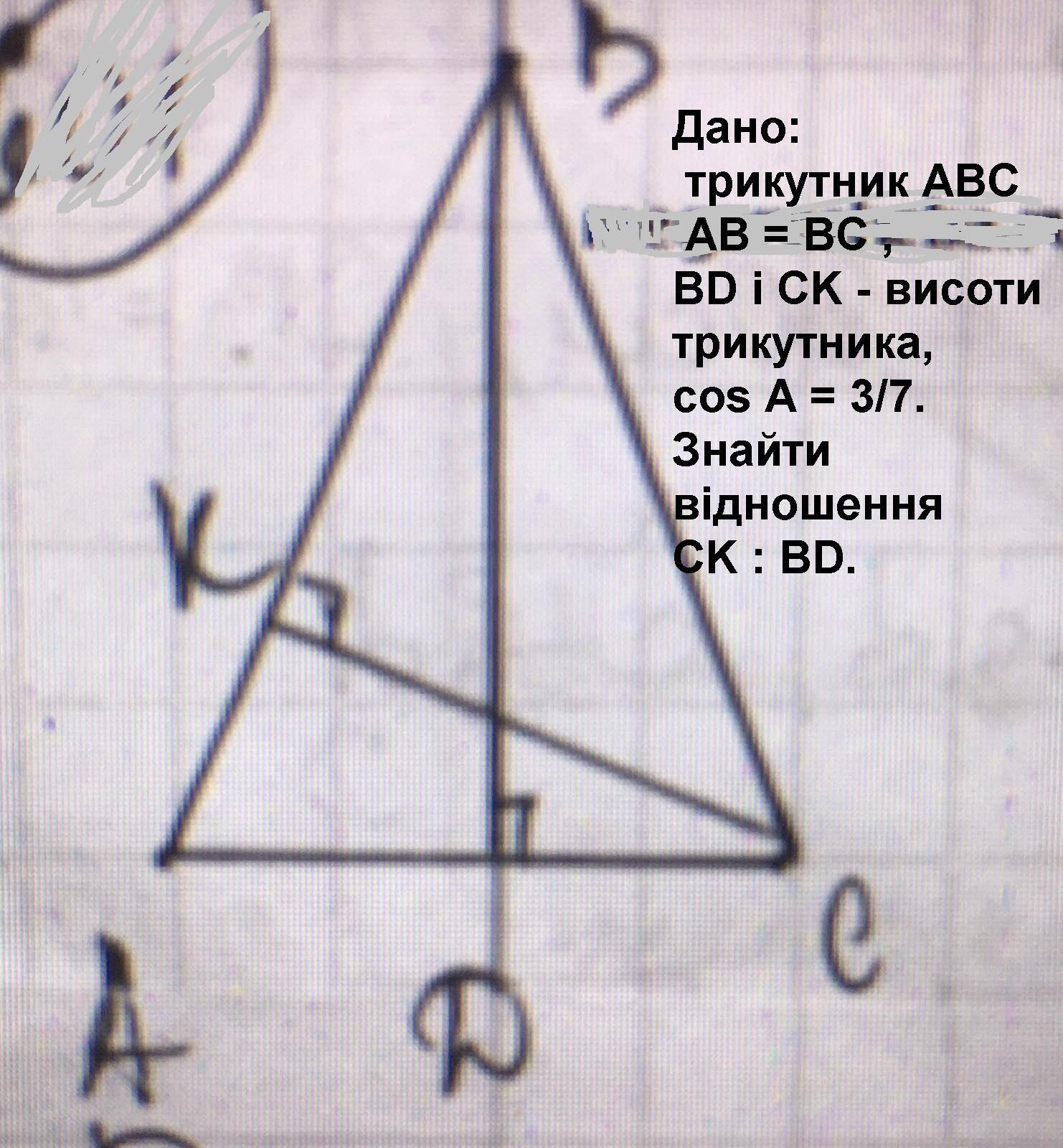
у трикутника ABC відомо, що AB = BC , BD і CK - висоти трикутника, cos A = 3/7. Знайдіть відношення CK : BD.
Ответы
Відповідь: CK/BD = 6/7 .
Пояснення:
Прямок. ΔABD ∼ ΔACK за гострим ∠А , який для них спільний .
Звідси AB/AC = BD/CK ; -------> AC/AB = CK/BD . AC = 2 * AD , бо
висота BD у рівнобереному ΔАВС ( АВ = ВС - за умовою ) , тому
2 * AD/AB = CK/BD ; -------> CK/BD = 2 * cosA = 2 * 3/7 = 6/7 .
В - дь : CK/BD = 6/7 .
Відповідь:
Дано:
трикутник ABC
AB = BC , BD і CK - висоти трикутника, cos A = 3/7.
Знайти відношення CK : BD.
Розв"язання:
так як АВ=ВС,то трикутник рівнобедрений й кут А=куту С
нехай ДС=3х,а ВС=7х
cos A = cos С = ДС/ВС= 3х/7х
АВ=ВС=7х; АД=ВС=7х; АД=3х=ДС; АС=6х
Sin С=ВД/ВС=ВД/7х ;Sin А = КС/АС=КС/6х ;Sin А=SinС тому ВД/7х=КС/6х,тому СК/ВД=6х/7х=6/7
ВІдповідь: СК:ВД ,як 6:7
Пояснення: