Сумма первых 17 членов арифметической прогрессии равна сумме первых 23 членов этой прогрессии. Найдите сумму первых 40 членов этой прогрессии

Ответы

Ответ дал: liftec74

Ответ: S(40)=0

Пошаговое объяснение:

Пусть 1-ый член равен у , а разность равна х

Тогда S(17)=(2x+16y)*17/2

S(23)=(2x+22y)*23/2

=>(2x+16y)*17 =(2x+22y)*23 =>17x+136y=23x+253y

6x=-117y

x=-19.5y

=> S(40)= (2x+39y)*40/2= (2*(-19.5y)+39y)*20=(-39y+39y)*20=0

Ответ дал: antonovm

Ответ:

0 ....................

Пошаговое объяснение:

Приложения:

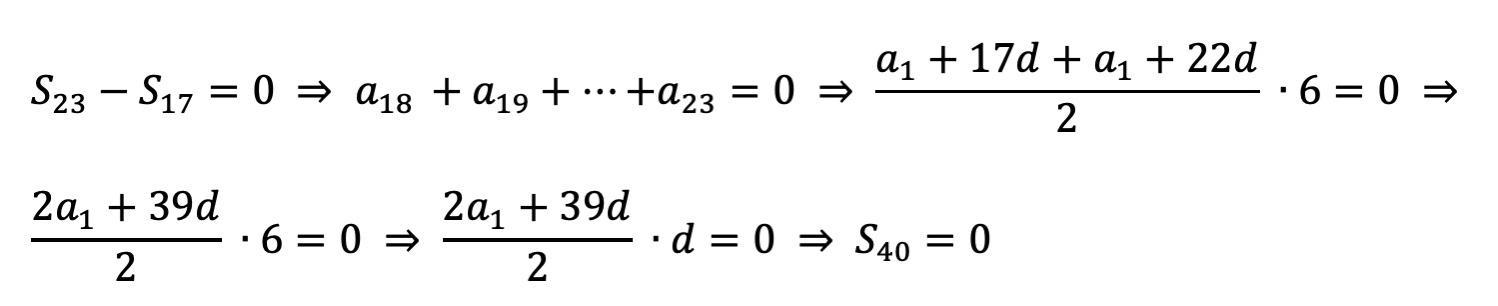
antonovm: Небольшое пояснение : члены прогрессии с 18 по23 образуют также прогрессию , первый член которой а(18) , а последний а(23) , поэтому их сумму можно найти по общей формуле ( полусумма первого и последнего , умноженная на их количество )

liftec74: Так на самом деле значительно проще , чем у меня.

antonovm: в последней строке вместо d надо , конечно , 40 поставить ( опечатка )

Похожие вопросы

Русский язык

1 год назад

Что представляет собой нынешняя молодежь? 100 слов

Литература

1 год назад

Випиши епітети з вірша Лесі Українки «як дитиною бувало..»

Физика

1 год назад

Для нагрівання 420 г металу від 30 до 45 °С потрібна кількість теплоти 1,12 кДж. Визначте, що це за метал. СРОЧНООООО!!!!!!!!!!!!!