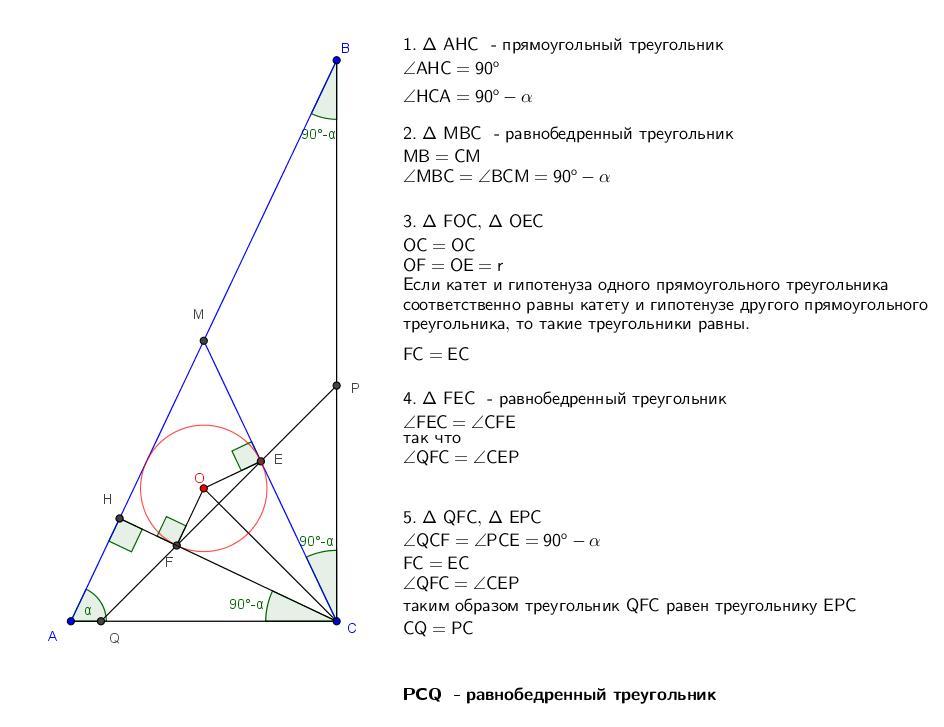
В прямоугольном треугольнике ABC с прямым углом C произведены высота CH и медиана CM. Круг, вписанный в треугольник MCH, касается сторон CM и CH в точках E и F. Прямая EF пересекает катеты треугольника ABC в точках P и Q. Докажите, что треугольник PCQ — равнобедренный.

Ответ:

треугольник PCQ — равнобедренный

Пошаговое объяснение:

1.  - прямоугольный треугольник

2.  - равнобедренный треугольник

3.

Если катет и гипотенуза одного прямоугольного треугольника

соответственно равны катету и гипотенузе другого прямоугольного

треугольника, то такие треугольники равны.

4.  - равнобедренный треугольник

так что

5.

таким образом треугольник QFC равен треугольнику EPC

PCQ  - равнобедренный треугольник