из одной точки окружности радиуса 6 см проведены две взаимно перпендикулярные равные хорды Найдите длину этих хорд
Ответы
Відповідь:
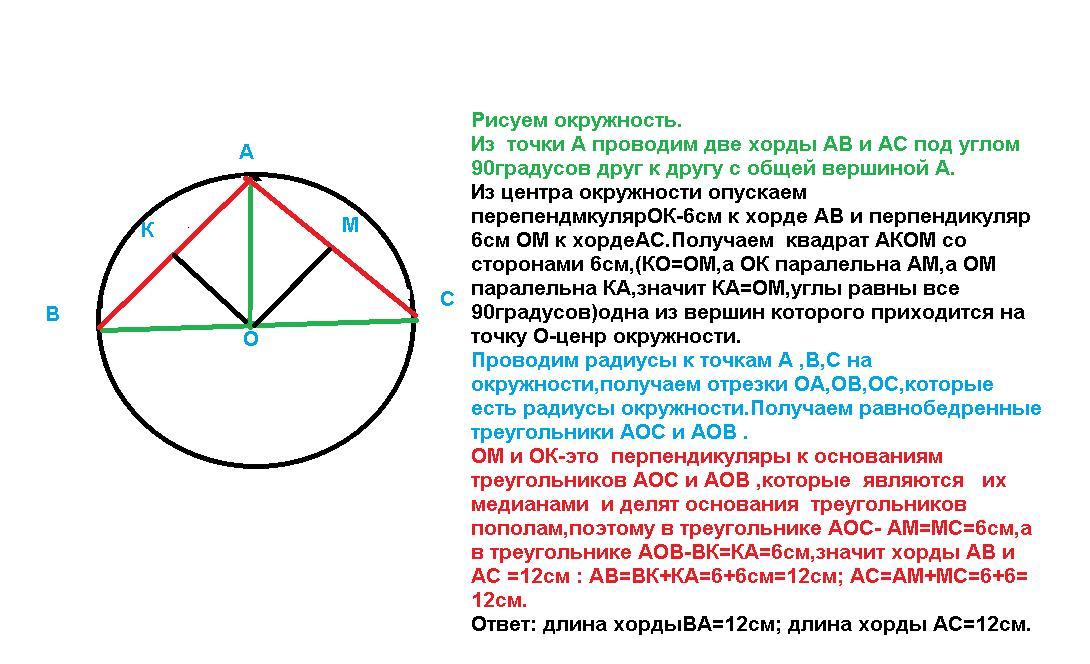
Рисуем окружность.
Из точки А проводим две хорды АВ и АС под углом 90градусов друг к другу с общей вершиной в точке А.
Из центра окружности опускаем перепендикуляр ОК-6см к хорде АВ и перпендикуляр 6см ОМ к хорде АС. Получаем квадрат АКОМ со сторонами 6см,(КО=ОМ,а ОК параллельна АМ,а ОМ параллельна КА,значит КА=ОМ,углы равны все 90градусов)одна из вершин которого приходится на точку О- центр окружности.
Проводим радиусы к точкам А ,В,С на окружности, получаем отрезки ОА,ОВ,ОС, которые есть радиусы окружности. Получаем равнобедренные треугольники АОС и АОВ .
ОМ и ОК-это перпендикуляры к основаниям треугольников АОС и АОВ ,которые являются их медианами и делят основания треугольников пополам, поэтому в треугольнике АОС- АМ=МС=6см,а в треугольнике АОВ-ВК=КА=6см,значит хорды АВ и АС =12см : АВ=ВК+КА=6+6см=12см; АС=АМ+МС=6+6=12см.
Ответ: длина хорды ВА=12см; длина хорды АС=12см.
Пояснення: