Задача :
" Запишите периодическую дробь 0,215(9) в виде конечной десятичной дроби ".
Что здесь требуется ? То есть , надо дробь округлить ?Или период отбросить ?
StarSpangledBanner:
Да, понимаю .Потому что период 0,(9) отделен от одного какая-то шаловливая разница в единичку в бесконечно далекой позиции в этом периоде.
Извините, что неграмотно пишу. Умная Клавиатура все коверкает.
Та ну, не парьтесь по этому поводу
А вам спасибо огромнейшее !!!
Та не за что здесь. Просто делюсь мыслями
a = 0 , 215(9) ; 1000a = 215,(9) = 215 + 0,(9) = 215 +1 = 216 ; a = 0,216
0,9 = 0,9 + 0,09 + 0,009 + ... = 0,9 /( 1 - 0,1) = 1 ( как сумма бесконечно убывающей геометрической прогрессии
Спасибо вам большое.
опечатка , не 0,9 , а 0 , (9)
Понимаю.
Ответы
Ответ дал:
1
Ответ: 0,216.
Объяснение:
0,215(9) = (2159-215)/9000 = 27/125 = 0,216.
Период равен 9 - один знак - одна девятка.
После запятой три знака - добавляем три нуля.
Получаем знаменатель 9000.
Приложения:
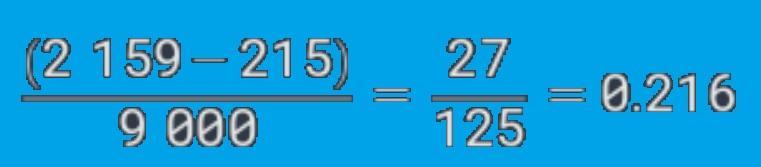
Похожие вопросы
1 год назад
1 год назад
1 год назад
1 год назад
2 года назад
2 года назад
8 лет назад
8 лет назад