Угол основания равнобедренной трапеции равен 60°, а диагональ равна 9 см. Найдите диаметр окружности вписанной трапеции

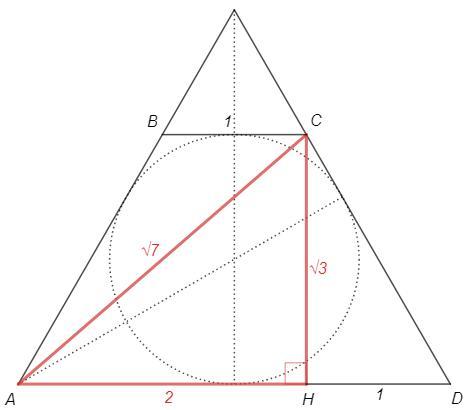
Трапеция ABCD - усеченный равносторонний треугольник.

Центр его вписанной окружности - точка пересечения биссектрис/высот/медиан.

Пусть основание 3. Тогда высота треугольника 3√3/2.

Диаметр вписанной окружности =2/3 высоты треугольника =√3

Диаметр вписанной окружности равен высоте трапеции, CH=√3

Понятно, что AH=2 и по т Пифагора AC=√7

CH/√3=AC/√7 => CH=9√3/√7 (см)