Помогите записать с дано и с полным решением,пожалуйста

Ответ:

∠САВ=160°

Объяснение:

Дано:

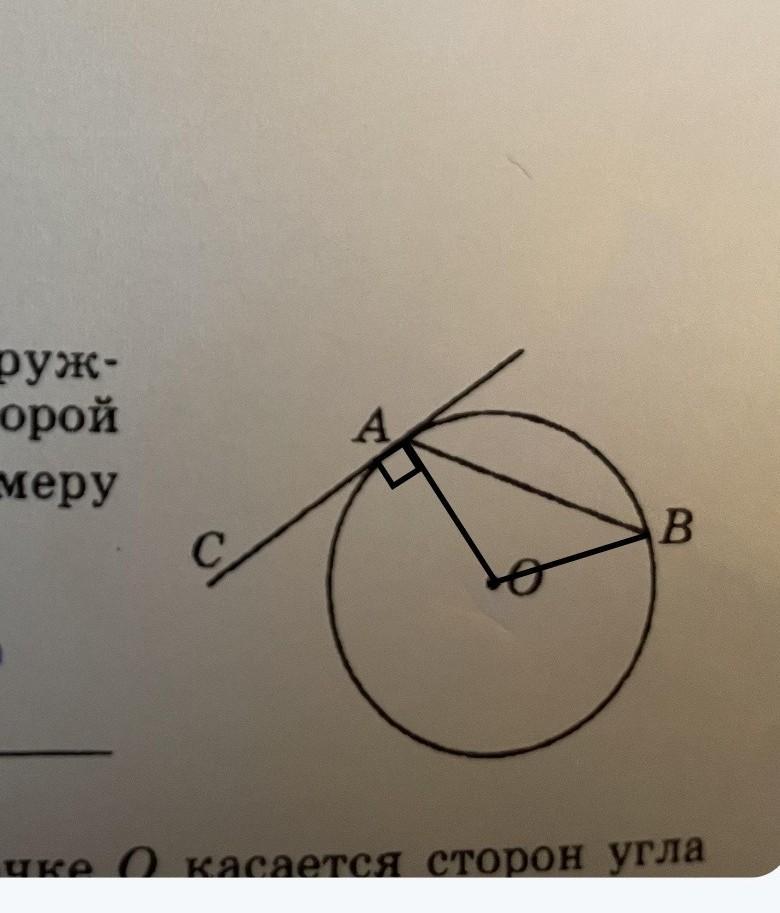
т.О- центр окружности

АВ- хорда

◡АВ=40°

СА- касательная

∠САВ=?

Решение:

∠АОВ=◡АВ=40°

∆АОВ- равнобедренный треугольник АО=ОВ=R.

В равнобедренном треугольнике углы при основании равны. (∠ОАВ=∠ОВА)

Сумма углов в треугольнике равна 180°

∠ОАВ=(180°-∠АОВ)/2=(180°-40°)/2=

=140°/2=70°

∠САО=90°, т.к. АС касательная

∠САВ=∠САО+∠ОАВ=90°+70°=160°