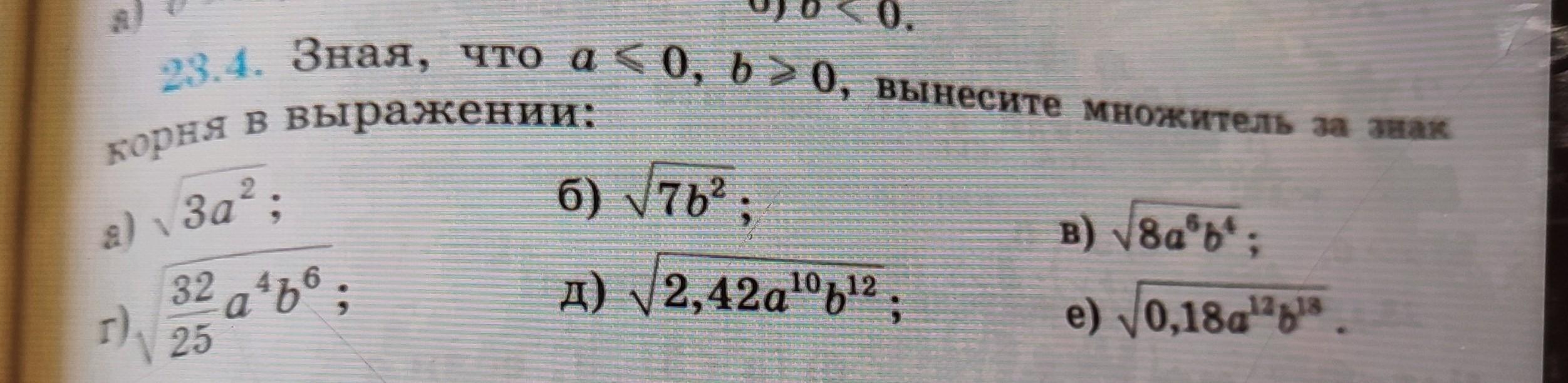Даю 100 балов
Помогите пожалуйста

Приложения:

Ответы

Ответ дал: NNNLLL54

Ответ:

Правило извлечения квадратного корня : $\bf \sqrt{a^2}=|\, a\, |$ ,

$\bf |\, a\,|=\left\{\begin{array}{l}\bf \ a\ ,\ esli\ a\geq 0\ ,\\\bf -a\ ,\ esli\ a < 0\ .\end{array}\right$

Запишем подкоренное выражение в виде квадрата выражения , а затем извлечём корень . Учтём, положительное или отрицательное выражение получим под знаком модуля .

$\bf a\leq 0\ ,\ \ b\geq 0\\\\1)\ \ \sqrt{3a^2}=|\, a\, |\cdot \sqrt3=-a\sqrt3\\\\\\2)\ \ \sqrt{7b^2}=|\, b\, |\sqrt7=b\sqrt7\\\\\\3)\ \ \sqrt{8\, a^6\, b^4}=\sqrt{2^2\cdot 2\cdot (a^3)^2\cdot (b^2)^2}=2\cdot |\underbrace{\bf a^3}_{\leq 0}|\cdot |\underbrace{\bf b^2}_{\geq 0}|\cdot \sqrt2=\\\\=2\cdot (-a^3)\cdot b^2\cdot \sqrt2=-2\, a^3\, b^2\sqrt2$

$\bf 4)\ \ \sqrt{\dfrac{32}{25}\, a^4\, b^6}=\sqrt{\dfrac{2^4\cdot 2}{5^2}\cdot (a^2)^2\cdot (b^3)^2}=\dfrac{2^2}{5}\cdot |\underbrace{\bf a^2}_{\geq 0}|\cdot |\underbrace{\bf b^3}_{\geq 0}|\cdot \sqrt{2}=\\\\=\dfrac{4}{5}\, a^2\, b^3\sqrt2$

$\bf 5)\ \ \sqrt{2,42\, a^{10}\,b^{12}}=\sqrt{2\cdot 1,1^2\cdot (a^5)^2\cdot (b^6)^2}=1,1\cdot |\, a^5\, |\cdot |\, b^6\, |\cdot \sqrt2=\\\\=1,1\cdot (-a^5)\cdot (b^6)\cdot \sqrt2=-1,1\, a^5\, b^6\sqrt2\\\\\\6)\ \ \sqrt{0,18\, a^{12}\, b^{13}}=\sqrt{2\cdot (0,3)^2\cdot (a^6)^2\cdot (b^6)^2\cdot b}=0,3\cdot |a^6|\cdot |b^6|\cdot \sqrt{2b}=\\\\=0,3\, a^6\, b^6\cdot \sqrt{2b}$

Приложения:

luzginkirill2010: Спа

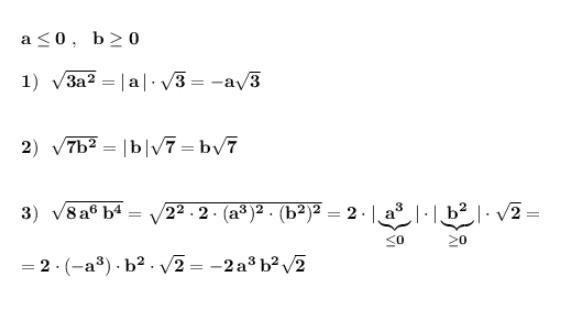
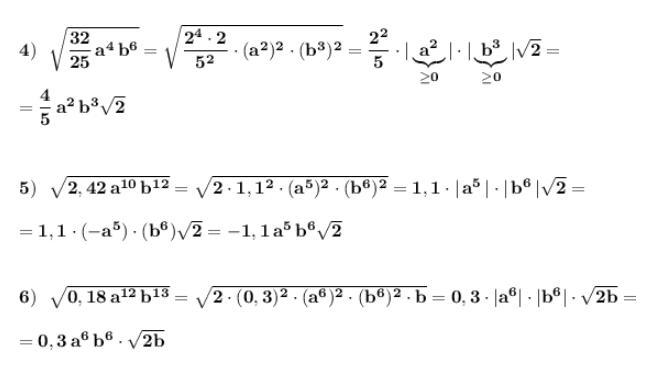
luzginkirill2010: Спасибо

luzginkirill2010: Конечно решение не совсем понятно, но ответы сошлись)

NNNLLL54: что же там непонятного ? что надо выражение писать в виде квадрата ? что модуль надо писать ? что модуль раскрывается в зависимости от знака подмодульного выражения ? спросите , отвечу

Похожие вопросы

Математика

1 год назад

Довжина одиничного відрізка координатного променя дорівнює 3 см. На цьому промені позначено точки К(50)іL(55). Якою є довжина відрізка KL?

Математика

1 год назад

ДАЮ СТО БАЛОВ ЗА 3 задания N° 1. Побудуйте переріз чотирикутної піраміди площиною, що проходить через вершину піраміди і діагональ основи. N° 2. Побудуйте переріз трикутної піраміди, що

Математика

1 год назад

12. Составьте уравнения и решите их. Выполните проверку. 118 329 435 860 64 907 m m m 17 620

Литература

1 год назад