В равнобедренном треугольнике ABC AB=AC=13 см, BC= 10 см. Найдите расстояние от точки пересечения медиан треугольника до вершины A

Ответ:

Расстояние от вершины А до точки пересечения медиан равно 8см.

Объяснение:

Медианы, пересекаясь, делятся точкой пересечения в отношении 2:1, считая от вершины.

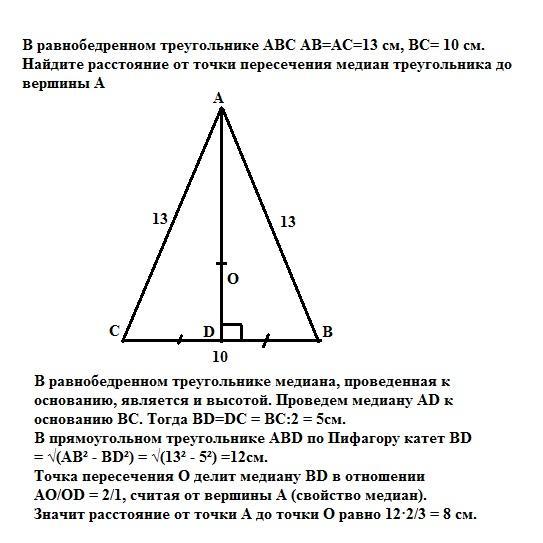
В равнобедренном треугольнике медиана, проведенная к основанию, является и высотой. Проведем медиану AD к основанию ВС. Тогда BD=DC = BC:2 = 5см.

В прямоугольном треугольнике АВD по Пифагору катет

BD = √(АВ² - BD²) = √(13² - 5²) =12см.

Точка пересечения О делит медиану BD в отношении

АО/ОD = 2/1, считая от вершины А (свойство медиан). Значит расстояние от точки А до точки О равно 12·2/3 = 8 см.