❗️❗️❗️Срочно❗️❗️❗️
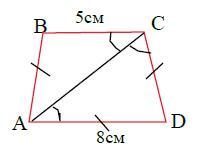
1. У рівнобічній трапеції діагональ є бісектрисою тупого кута, а основи дорівнюють 5 см і 8 см. Знайди периметр трапеції

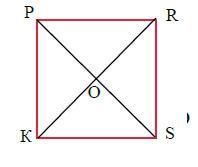
2. Діагоналі квадрата KPRS перетинаються в точці О.
Знайди діагональ KR, якщо PS + OR = 12 см


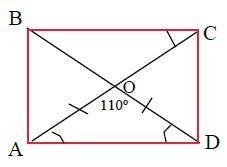
3. У прямокутнику діагоналі AC і BD перети­нають­ся в точці О.

Знайди кут ACB, якщо кут AОD = 110°

Ответ:

Объяснение:

1. В равнобедренной трапеции ABCD  ∠ВСА = ∠DCA, т.к. АС - биссектриса.
2. ∠ВСА = ∠CAD как накрест лежащие при параллельных: ВС ║AD и секущей АС.
3. В ΔACD ∠ВСА = ∠CAD, значит, ΔACD - равнобедренный и
CD = AD = 8см
4. Трапеция ABCD - равнобедренная, следовательно, АВ = CD = 8см

Р(abcd) = 5 +8*3 = 5 +24 = 29(см)
__________________
Диагонали квадрата равны и в точке пересечения делятся пополам.
PS = KR или  PO = OS  =  KO = OR.
По условию,  PO + OS +OR = 12(см)
PO = OS =  OR = 12*3 = 4(см)
KR = 4*2 = 8(см)

______________
1. Диагонали прямоугольника равны и в точке пересечения делятся пополам.
АО = OD, значит ΔAOD - равнобедренный и, следовательно, углы при основании равны.
∠AOD = ∠ODA = (180° -110°)/2 = 70°/2 = 35°
(сумма всех углов Δ-ка = 180°)

2. ∠ACB = ∠CAD = 35°  как накрест лежащие при параллельных  ВС║AD и секущей АС.