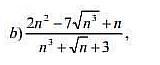Предмет: Алгебра
Автор: fctdgsygfdhngfxzgsac
Вопрос задан 1 год назад

< >

Знайти границі послідовностей. n --> ∞

Приложения:

Ответы

Ответ дал: tаtyana

1

Разделим числитель и знаменатель на старшую степень, здесь это n³.

$\\lim_{n \to \infty} \frac{\frac{2}{n^2} -\frac{7\sqrt{n^3} }{n^3} +\frac{n}{n^3} }{\frac{n^3}{n^3}+\frac{\sqrt{n} }{n^3} +\frac{3}{n^3} } = \lim_{n \to \infty}\frac{\frac{2}{n^2}-7\sqrt{\frac{n^3}{n^6} } +\frac{1}{n^2} }{1+\sqrt{\frac{n}{n^6} }+\frac{3}{n^3} } =\\ \\ = \lim_{n \to \infty} \frac{\frac{2}{n^2}-7\sqrt{\frac{1}{n^3} }+\frac{1}{n^2} }{1+\sqrt{\frac{1}{n^5} } +\frac{3}{n^3} } =\frac{0}{1} =0$

Аноним: ну что, вот и 1 человек из 19 как у вас говорят отдосвидулился

Аноним: поехал процесс

Аноним: мечты сбудутся. газпром. https://ibb.co/8KnKmy2

Аноним: да мне посрать

Похожие вопросы

Кыргыз тили

1 год назад

Қазіргі заманда қандай кәсіппен айналысқан тиімді.Срочно

Физика

1 год назад

1. Чому дорівнює довжина важеля, якщо на його кiнцi дiють сили 2 Н та 18 Н, а відстань точки опори від більшої сили дорівнює 10 см.

Литература

1 год назад

Краткий пересказ о защитников древнего Отрара

Математика

1 год назад

Знайдіть обернене число до 22/35 і 21/44

Українська мова

2 года назад

прочитайте текст: помогите пожалуйста

Геометрия

2 года назад

14. Постройте ромб по: а) стороне и диагонали Пожалуйста

Математика

8 лет назад

Какое наибольшее число пирожных по 6 руб. можно купить ,если имеется:20 р.,35 р.,40 руб.,50 р.?

Физика

8 лет назад

Какая совершается работа при равномерном подъёме груза массой 1 кг на высоту 1м?