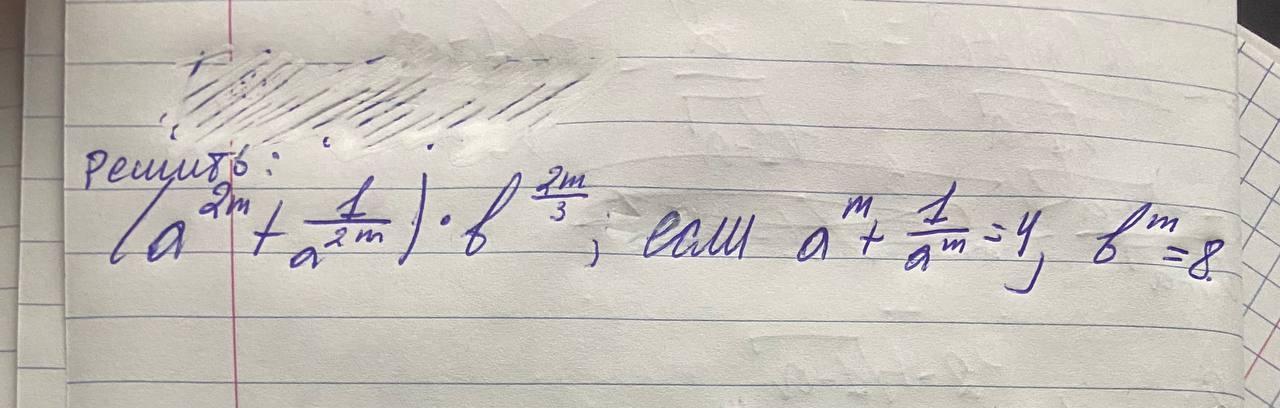найдите значения (а^2m+1/a^2m)*b^2m, если a^m+1/a^m=4, b^m=8

Ответ:

.

Для нахождения значения выражения (a^(2m+1)/a^(2m)) * b^(2m), сначала рассмотрим данные:

1. a^(m+1)/a^m = 4

2.в^m=8

1. a^(m+1)/a^m = a^m * a/a^m = a (поскольку a^m / a^m = 1)

2. b^m=8 означает, что b=2, так как 2^m=8.

(a^(2m+1)/a^(2m)) * b^(2m) = (4^(2m+1)/4^(2m)) * 2^(2m)

(4^(2m+1)/4^(2m)) = 4^(2m+1-2m) =

2^(2m) = (2^m)^2 = 8^2 =64

4*64 = 256

Следовательно, значение выражения (a^(2m+1)/a^(2m)) * b^(2m) равно 256