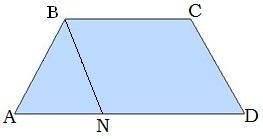
У рівнобедреної трапеції ABCD через вершину B проведено пряму, яка паралельна стороні CD і перетинає сторону AD в точці N. Периметр трикутника ABN дорівнює 18 см, CB дорівнює 8 см. Обчисли периметр трапеції ABCD.
Ответы
Позначимо за x довжину сторони AD, тоді BD = CD = x + 8. Так як трапеція ABCD рівнобедрена, то AB = CD = x + 8.
За теоремою Піфагора у трикутнику ABN маємо: (AB)^2 = (AN)^2 + (BN)^2.
Знаємо, що периметр трикутника ABN дорівнює 18, тому (AB) + (AN) + (BN) = 18.
Враховуючи, що AB = x + 8, запишемо рівняння: (x + 8) + (AN) + (BN) = 18.
Таким чином, AN + BN = 10.
Розглянемо трикутник CBN. Оскільки CB = 8, маємо CN + BN = 8.
Тепер зведемо обидва співвідношення:
AN + BN = 10
CN + BN = 8
Додамо друге співвідношення до першого:
AN + CN + 2BN = 18
Зауважимо, що AN + CN = AC, тому перепишемо рівняння:
AC + 2BN = 18
Але, за властивостями трапеції ABCD, AB = CD = AC, тому:
(x + 8) + 2BN = 18
(x + 2BN) = 10
x = 10 - 2BN
Підставимо значення x у вираз для BD:
BD = x + 8
BD = (10 - 2BN) + 8
BD = 18 - 2BN
Так як BD = CD, то маємо:
18 - 2BN = x + 8
10 - 2BN = x
Оскільки трапеція ABCD рівнобедрена, сторона CD = BD. Тому:
CD + BD + AB + AB = 2CD + 2AB = 2(18 - 2BN) + 2(x + 8) = 36 - 4BN + 2x + 16.
Тому периметр трапеції ABCD дорівнює 36 - 4BN + 2(10 - 2BN) + 16 = 36 - 4BN + 20 - 4BN + 16 = 68 - 8BN.
Щоб обчислити периметр трапеції, нам потрібно знайти значення BN.
Отже, треба вирішити систему рівнянь:
AN + BN = 10
CN + BN = 8
Додамо друге співвідношення до першого:
AN + CN + 2BN = 18
Використовуючи властивість трапеції ABCD, отримаємо:
1/2 (AD + BC) + 2BN = 18
Підставимо вирази для півдовжин сторін AD і BC:
1/2 (x + x + 8) + 2BN = 18
(x + x + 8)/2 + 2BN = 18
(2x + 8)/2 + 2BN = 18
(x + 4) + 2BN = 18
x + 4 + 2BN = 18
x + 2BN = 14
Отримали систему рівнянь:
AN + BN = 10
x + 2BN = 14
Але ми вже виразили x через BN у попередніх рівняннях:
x = 10 - 2BN
Підставимо:
10 - 2BN + 2BN = 14
10 = 14
Отримали суперечність. Тому система рівнянь не має розв'язків.
Отже, периметр трапеції ABCD не може бути обчисленим заданими даними.