Продиференціювати функції.

Знайти похідну .......

Продифференцировать функции.

Найти производную .......

Приложения:

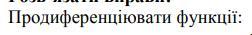
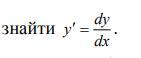
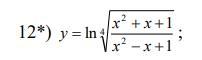
Ответы

Ответ дал: natalyabryukhova

Ответ:

8. $\displaystyle y'=-\frac{12}{1-9x^2}$

12. $\displaystyle y'=\frac{1-x^2}{2(x^4+x^2+1)}$

Объяснение:

Найти производную:

8. $\displaystyle \bf y=ln\left(\frac{1-3x}{1+3x}\right)^2$

Производная частного:

$\boxed {\displaystyle \bf \left(\frac{u}{v}\right)'=\frac{u'v-uv'}{v^2} }$

$\displaystyle y'=\frac{1}{\left(\frac{1-3x}{1+3x}\right)^2 } \cdot \left(\left(\frac{1-3x}{1+3x}\right)^2 \right)'=\frac{(1+3x)^2}{(1-3x)^2} \cdot2\left(\frac{1-3x}{1+3x}\right)\cdot\left(\frac{1-3x}{1+3x}\right)'=\\\\\\=2\cdot\frac{1+3x}{1-3x}\cdot \frac{-3\cdot(1+3x)-(1-3x)\cdot3}{(1+3x)^2} =\\\\\\=\frac{2}{1-3x}\cdot \frac{-3-9x-3+9x}{1+3x} =-\frac{12}{1-9x^2}$

12. $\displaystyle \bf y=ln\sqrt[4]{\displaystyle \bf\frac{x^2+x+1}{x^2-x+1} }$

$\displaystyle y'=\frac{1}{\left(\frac{x^2+x+1}{x^2-x+1}\right)^{\frac{1}{4}}} \cdot \left(\left(\frac{x^2+x+1}{x^2-x+1}\right)^{\frac{1}{4} } \right)'=\\ \\\\=\frac{(x^2-x+1)^{\frac{1}{4} }}{(x^2+x+1)^\frac{1}{4} }\cdot \frac{1}{4} \cdot\left(\frac{x^2+x+1}{x^2-x+1}\right)^{-\frac{3}{4}}\cdot \left(\frac{x^2+x+1}{x^2-x+1}\right)'=$

$\displaystyle =\frac{(x^2-x+1)^{\frac{1}{4} }}{(x^2+x+1)^\frac{1}{4} }\cdot \frac{1}{4} \cdot\left(\frac{x^2-x+1}{x^2+x+1}\right)^{\frac{3}{4}}\cdot \frac{(2x+1)(x^2-x+1)-(x^2+x+1)(2x-1)}{(x^2-x+1)^2}=\\\\\\=\frac{1}{4}\cdot \frac{x^2-x+1}{x^2+x+1}\cdot \frac{2x^3-2x^2+2x+x^2-x+1-2x^3-2x^2-2x+x^2+x+1}{(x^2-x+1)^2} =\\\\\\=\frac{-2x^2+2}{4(x^2+1+x)(x^2+1-x)} =\frac{1-x^2}{2(x^4+2x^2+1-x^2)} =\frac{1-x^2}{2(x^4+x^2+1)}$

Аноним: откуда скопипастили? 8й номер какой-то?

Ответ дал: yugolovin

Ответ: $y'=-\dfrac{x^2-1}{2(x^4+x^2+1)}.$

Решение. $y=\ln\sqrt[4]{\dfrac{x^2+x+1}{x^2-x+1}}=\dfrac{1}{4}(\ln(x^2+x+1)-\ln(x^2-x+1));$

$y'=\dfrac{1}{4}\left(\dfrac{2x+1}{x^2+x+1}-\dfrac{2x-1}{x^2-x+1}\right)=\dfrac{1}{4}\cdot\dfrac{(2x+1)(x^2-x+1)-(2x-1)(x^2+x+1)}{(x^2+x+1)(x^2-x+1)}=$

$=\dfrac{2x^3-2x^2+2x+x^2-x+1-(2x^3+2x^2+2x-x^2-x-1)}{4((x^2+1)^2-x^2)}=$

$=\dfrac{-2x^2+2}{4(x^4+x^2+1)}=-\dfrac{(x^2-1)}{2(x^4+x^2+1)}.$

Мы воспользовались свойствами логарифма:

если a>0, b>0, то $\ln\sqrt[n]{\dfrac{a}{b}}=\ln\left(\dfrac{a}{b}\right)^{1/n}=\dfrac{1}{n}\ln \dfrac{a}{b}=\dfrac{1}{n}(\ln a-\ln b).$

В нашем случае $a=x^2+x+1 > 0$ при всех x, $b=x^2-x+1 > 0$ при всех x (можно убедиться этом вычислив дискриминанты и убедившись в их отрицательности). Впрочем, если бы мы не были уверены в положительности a и b, мы приписали бы модули, которые все равно исчезают при дифференцировании.