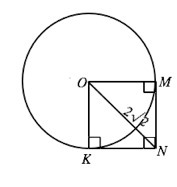
MN и NK - отрезки касательных, проведённых к окружности с центром О, угол MNK=90 град. Найдите радиус окружности, если ОN=2 корень из 2 см.

Радиус, проведенный в точку касания, перпендикулярен касательной. ОК⊥NK,  OM⊥MN. Угол MNO=90° по условию. 

В четырехугольнике KNMO три углы прямые, ⇒ KNMO - квадрат,

 и ОN- его диагональ. 

ОК=NK,  ∆ OKN равнобедренный прямоугольный, его острые углы  равны 45°.

ОК=ON•sin45°=2√2•√2/2=2.

Тот же результат получим, воспользовавшись для нахождения радиуса ОК т.Пифагора